Archives de catégorie : géométrie

géométrie

géométrie projective, exemple de calculs(2)

\bullet Soit D une droite affine d’équation f et soient a, b deux points distincts du plan affine. On suppose que D coupe (ab) en m. On a les propriétés suivantes :

1) On a m =\dfrac{f(b)a - f(a)b}{f(b) - f(a)}.

2) On a la formule :\dfrac{\overline{ma}}{\overline{mb}}=\dfrac{f(a)T(b)}{f(b)T(a)}

\bullet \underline{\text{Théorème}\; \text{de}\; \text{Thalès}}

Soient A,B,C trois droites parallèles. Deux droites D,D' coupent respectivement A,B,C en a, b, c ; a', b', c'.

On a la formule : \dfrac{\overline{ab}}{\overline{ac}}=\dfrac{\overline{a'b'}}{\overline{a'c'}}

En effet, soit f une équation de A, on a:
\dfrac{\overline{ab}}{\overline{ac}}=\dfrac{f(b)T(c)}{f(c)T(b)} et \dfrac{\overline{a'b'}}{\overline{a'c'}} =\dfrac{f(b')T(c')}{f(c')T(b')} . Mais, commeB = (bb') est parallèle à A on a f(b)T(b') =f(b')T(b) et de même, f(c)T(c') = f(c')T(b).
Le résultat s’ensuit.

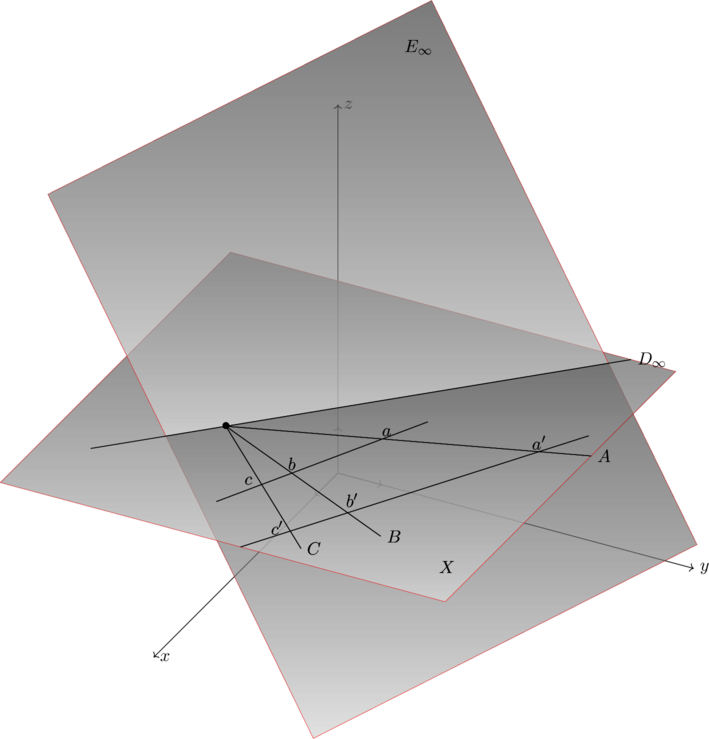
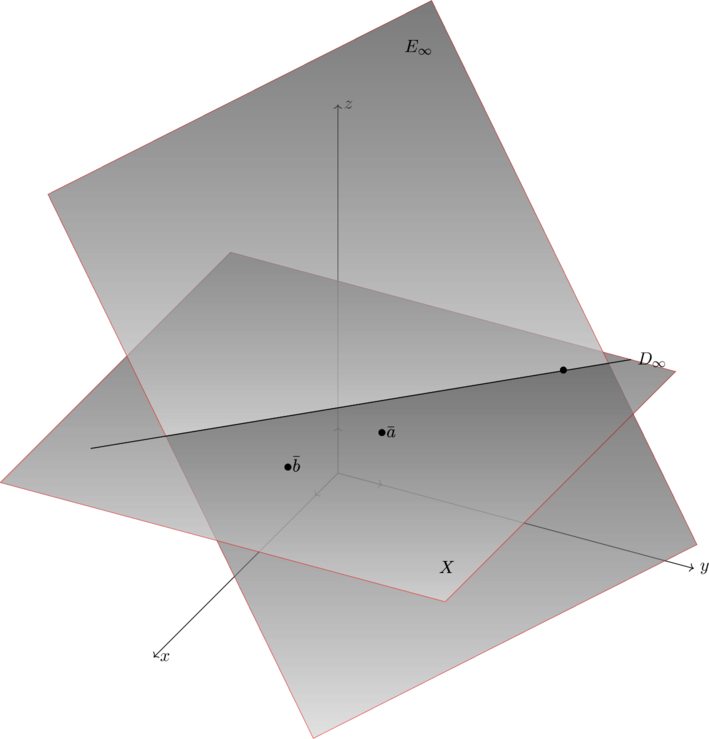
Exemple, situation 1, (T=x+y+z).

Rendered by QuickLaTeX.com

Continuer la lecture de géométrie projective, exemple de calculs(2) →
géométrie

géométrie projective: Exemple de calculs

Résumé:
\bullet On se donne
une forme linéaire non nulle T \in E^* et on considère l’hyperplan vectoriel E_{\infty} défini par T. On pose P(E_{\infty}) =D_{\infty} (c’est un hyperplan projectif) et X = P(E )\setminus D_{\infty }

L’application qui à \overrightarrow{u} \in E_{\infty} et \bar{x}\in X associe \overrightarrow{u}.\bar{x} = \overline{x + T(x)\overrightarrow{u}} est bien définie. C’est une opération de E_{\infty} sur X , simplement transitive, de sorte qu’elle fait de X un espace affine sous E_{\infty}.
Si \bar{a}, \bar{b} sont deux points de X, le vecteur \overrightarrow{ab} est le vecteur de E_{\infty} défini par \overrightarrow{ab}=\dfrac{b}{T(b)}-\dfrac{a}{T(a)} , il est indépendant du choix des représentants des points.

Situation 1 (T=x+y+z)
Soit a(0,1,1) et b(2,0,1), \overrightarrow{ab}=(\dfrac{2}{3},-\dfrac{1}{2}, -\dfrac{1}{6})

Rendered by QuickLaTeX.com

Continuer la lecture de géométrie projective: Exemple de calculs →

géométrie

Exercices sur les angles.

 

1–Les hauteurs dans un triangle

Soit ABC un triangle quelconque, H le point d’intersection des hauteurs issues de A et B.

Rendered by QuickLaTeX.com

Les points A,B,A’,B’ se situent sur un même cercle, on en déduit:

(\overrightarrow{B'A'},\overrightarrow{B'B})=(\overrightarrow{AA'},\overrightarrow{AB})

Les points C,A’,H et B’ se situent sur un même cercle, on en déduit:

(\overrightarrow{B'C},\overrightarrow{B'A'})=(\overrightarrow{HC'},\overrightarrow{HA})

La mesure de l’angle (\overrightarrow{C'A},\overrightarrow{C'H}) est donc \dfrac{\pi}{2} ce qui démontre le concours des hauteurs dans un triangle.

2–Les longueurs des côtés d’un triangle sont proportionnelles aux sinus des angles opposés
Continuer la lecture de Exercices sur les angles. →