Vocabulaire

les mots clés ! (en cours de rédaction !)

Ci-dessous les définitions des termes les plus couramment utilisés en mathématiques, essentiellement issues du Ramis Tome1  :

\textlinb{a}

Appartenance : On appelle appartenance la relation binaire que l’on écrit x \in y et que l’on lit « x est un élément de y « .

Application: On appelle application toute correspondance dont le graphe est fonctionnel et dont l’ensemble de définition coïncide avec l’ensemble de départ.

Application croissante : Soient (E,\preccurlyeq ) et (F,\leq) deux ensembles ordonnés, on appelle application croissante toute application f : E\rightarrow F telle que : \forall (x,y) \in E^2 \;\;x\preccurlyeq y \Rightarrow f(x)\leq f(y).

Assertion : On appelle assertion tout énoncé ne contenant pas de variable ne pouvant prendre que l’une des deux valeurs logiques « Vrai » ou « Faux ».
Continuer la lecture de les mots clés ! (en cours de rédaction !) →

géométrie

Uniquement avec les aires…

Pour commencer deux petits lemmes sur les aires :

\bullet Soient ABC et ABD deux triangles tels que (AB) et (DC) soient parallèles, alors \mathscr{A}(ABC)=\mathscr{A}(ABD)

Rendered by QuickLaTeX.com

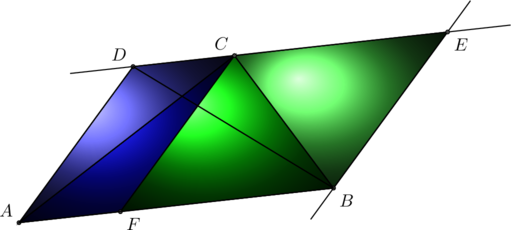
On trace les parrallèles à (AB) et (AD) , elles se coupent en E, et l’aire de chaque triangle est égale à la moitié de celle du parallèlogramme ABED.

\bullet Soit ABC un triangle, Q un point de (CB) et P un point de (AQ), alors \dfrac{\overline{QC}}{\overline{QB}}=\dfrac{\mathscr{A}(QCA)}{\mathscr{A}(QBA)}…. =\dfrac{\mathscr{A}(QCP)}{\mathscr{A}(QBP)} pour les mêmes raisons… =\dfrac{\mathscr{A}(PCA)}{\mathscr{A}(PBA)} par différence (chevron)

Rendered by QuickLaTeX.com

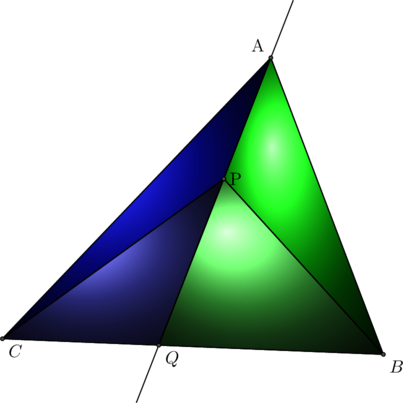
On utilise le fait que ces triangles ont le même hauteur.

Continuer la lecture de Uniquement avec les aires… →

géométrie

Birapport (partie 1)

Birapport de quatre points:

Définition:

Soit D une droite projective et soient a,b,c,d quatre points de D, avec a,b,c distincts.
Soit h l’unique homographie de D surP^1(k) définie par h(a) = \infty, h(b) = 0, h(c) = 1.
On appelle birapport des quatre points a,b,c,d pris dans cet ordre l’élément h(d) \in P^1(k) = k \cup {\infty} et on le note [a,b,c,d].
Soit f : d \rightarrow d' une homographie. On a l’égalité :
[a,b,c,d] = [f(a), f(b), f(c), f(d)] .

Les perspectives seront par la suite des homographies particulièrement utilisées ainsi que les incidences : Soit D une droite et m un point n’appartenant pas à D. On appelle incidence l’ application qui à toute droite \delta passant par m associe l’unique point d’intersection x de D et \delta.

Calcul du birapport:

Soit D une droite projective et soient a,b,c,d quatre points de D, avec a,b,c distincts, on a la formule suivante:
Continuer la lecture de Birapport (partie 1) →

Une journée sans Maths …