Statistiques
On cherche à étudier le caractère aléatoire de ![]() expériences fournissant les résultats chiffrés
expériences fournissant les résultats chiffrés ![]() . Les
. Les ![]() expériences sont réalisées à l’identique et indépendamment les unes des autres.
expériences sont réalisées à l’identique et indépendamment les unes des autres.
Nous faisons donc l’hypothèse que l’observation ![]() provient de
provient de ![]() variables aléatoires
variables aléatoires ![]() identiquement distribuées. La famille
identiquement distribuées. La famille ![]() est appelée un
est appelée un ![]() -échantillon et la loi commune des
-échantillon et la loi commune des ![]() est notée
est notée ![]() . L’aléa lié à notre expérience est tel que
. L’aléa lié à notre expérience est tel que ![]() .
.
Le problème fondamental de la Statistique est de déterminer la loi commune des ![]() supposée inconnue à partir des résultats
supposée inconnue à partir des résultats ![]() . On ne donnera pas de réponse absolue, on cherchera à déterminer une réponse approchée « la plus probable » selon des critères définis à l’avance.
. On ne donnera pas de réponse absolue, on cherchera à déterminer une réponse approchée « la plus probable » selon des critères définis à l’avance.
Pour obtenir des résultats précis et intéressants, nous faisons un certain nombre d’hypothèses liées à l’expérience effectuée sur la loi commune ![]() des variables
des variables![]() de l’échantillon, les différentes lois considérées possibles a priori pour les variables
de l’échantillon, les différentes lois considérées possibles a priori pour les variables ![]() sont les
sont les ![]() ,
, ![]() (on prédéfinit une famille de loi avec lesquelles il semble très probable de devoir travailler)
(on prédéfinit une famille de loi avec lesquelles il semble très probable de devoir travailler)
On cherche alors à déterminer le paramètre ![]() inconnu pour lequel
inconnu pour lequel ![]() .
.
Exemple de choix: ![]()
La probabilité d’obtenir une observation ![]() dépend du paramètre
dépend du paramètre ![]() du modèle.
du modèle.
![]()
![]() On appelle estimateur du maximum de vraisemblance le paramètre
On appelle estimateur du maximum de vraisemblance le paramètre ![]() pour lequel l’observation est la plus vraisemblable (probable ).
pour lequel l’observation est la plus vraisemblable (probable ).
Exemple 16
Le palmier à huile est sujet à une maladie appelée le blast. Cette variété de palmier apparait sous forme de palmiers jumeaux. Dans un champ comprenant ![]() tels couples de palmiers, on a décompté 242 couples sains, 185 couples composés d’un palmier malade et d’un palmier sain et 73 couples de palmiers malades tous les deux. A combien estimer la probabilité
tels couples de palmiers, on a décompté 242 couples sains, 185 couples composés d’un palmier malade et d’un palmier sain et 73 couples de palmiers malades tous les deux. A combien estimer la probabilité ![]() pour un palmier d’être malade ?
pour un palmier d’être malade ?
On doit, pour être en mesure de faire cette estimation, faire une hypothèse sur la transmission de la maladie d’un palmier à son jumeau.
L’hypothèse que l’on veut tester, ![]() , est que la maladie ne se transmet pas.
, est que la maladie ne se transmet pas.
Alors, si ![]() représente la probabilité pour qu’un pied soit malade, et si X est la variable aléatoire qui désigne le nombre de pieds malades dans un couple (X vaut 0, 1 ou 2), on a :
représente la probabilité pour qu’un pied soit malade, et si X est la variable aléatoire qui désigne le nombre de pieds malades dans un couple (X vaut 0, 1 ou 2), on a :
![]() (faire un arbre !)
(faire un arbre !)
Si l’on observe ![]() couples de palmiers jumeaux, on testera donc si la loi de
couples de palmiers jumeaux, on testera donc si la loi de ![]() où
où ![]() est le nombre de couples dont les deux éléments sont malades ,
est le nombre de couples dont les deux éléments sont malades , ![]() le nombre de couples comportant un seul pied malade,
le nombre de couples comportant un seul pied malade, ![]() le nombre de couples dont aucun pied n’est malade, est une loi multinomiale de paramètres
le nombre de couples dont aucun pied n’est malade, est une loi multinomiale de paramètres ![]() .
.
Préalablement à l’ajustement, il faudra estimer ![]() .
.
La vraisemblance s’obtient en remplaçant dans ![]() ,
, ![]() par 73,
par 73, ![]() par 185,
par 185, ![]() par 242, ce qui donne une fonction de
par 242, ce qui donne une fonction de ![]() seul.
seul.
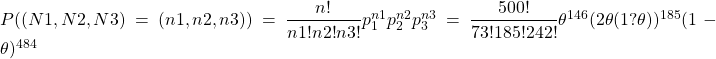
L’estimateur du maximum de vraisemblance de ![]() est la valeur qui rend cette fonction de
est la valeur qui rend cette fonction de ![]() aussi grande que possible. On obtient généralement cette valeur, qui rend la vraisemblance maximum, en cherchant le maximum du logarithme de la vraisemblance puisque la fonction Logarithme est monotone croissante.
aussi grande que possible. On obtient généralement cette valeur, qui rend la vraisemblance maximum, en cherchant le maximum du logarithme de la vraisemblance puisque la fonction Logarithme est monotone croissante.
On note ![]() la vraisemblance et
la vraisemblance et ![]() son logarithme. Ici
son logarithme. Ici ![]() vaut :
vaut :
![]()
![]()
![]()
![]()
On obtient le maximum de ![]() en dérivant
en dérivant ![]() par rapport à
par rapport à ![]()
![]() qui s’annule pour
qui s’annule pour ![]()
On a vu que 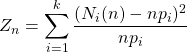 converge en loi vers la loi du
converge en loi vers la loi du ![]() à
à ![]() degrés de liberté, ici un paramètre (
degrés de liberté, ici un paramètre (![]() ) e été estimé.
) e été estimé.
avec les valeurs estimées de ![]() , on obtient
, on obtient ![]()
Or pour une loi ![]() on lit dans la table fournie en annexe
on lit dans la table fournie en annexe ![]()
12.55>3.84, on rejette ![]() , on ne peut pas affirmer que la maladie ne se transmet pas.
, on ne peut pas affirmer que la maladie ne se transmet pas.
![]() La méthode du maximum de vraisemblance est la méthode la plus naturelle pour estimer
La méthode du maximum de vraisemblance est la méthode la plus naturelle pour estimer ![]() à partir de
à partir de ![]() observations, mais son utilisation est souvent délicate aussi on préfèrera étudier une fonction de la forme
observations, mais son utilisation est souvent délicate aussi on préfèrera étudier une fonction de la forme ![]() dépendant de
dépendant de ![]() , c’est-à-dire en fait de la loi
, c’est-à-dire en fait de la loi ![]() .
.
Une telle fonction ![]() appelée estimateur est telle que la variable
appelée estimateur est telle que la variable ![]() est censée nous donner une valeur approchée de
est censée nous donner une valeur approchée de ![]() .
.
Un bon estimateur doit au moins vérifier les deux caractéristiques suivantes:
On dit que ![]() est une suite d’estimateurs \textbf{sans biais} pour
est une suite d’estimateurs \textbf{sans biais} pour ![]() si
si ![]() :
:
On dit que ![]() est une \textbf{suite convergente} d’estimateurs pour
est une \textbf{suite convergente} d’estimateurs pour ![]() si
si ![]()
Il est très classique de devoir estimer l’espérance et la variance de ![]() . Dans un modèle de Bernoulli par exemple, l’espérance caractérise la loi. Dans un modèle gaussien, l’espérance et la variance caractérisent la loi.
. Dans un modèle de Bernoulli par exemple, l’espérance caractérise la loi. Dans un modèle gaussien, l’espérance et la variance caractérisent la loi.
Estimateur pour l’espérance : ![]()
Alors ![]() est une suite convergente et sans biais d’estimateurs pour
est une suite convergente et sans biais d’estimateurs pour ![]()
Estimateur pour la variance : ![]()
![]() est convergent mais
est convergent mais ![]() ainsi on utilisera de préférence
ainsi on utilisera de préférence ![]() qui lui est un estimateur sans biais et convergent de la variance.
qui lui est un estimateur sans biais et convergent de la variance.
![]() Intervalles de confiance:
Intervalles de confiance:
En statistique on ne cherche pas à déterminer exactement ![]() , on se contente d’un intervalle déterminée à partir de
, on se contente d’un intervalle déterminée à partir de ![]() auquel appartient « vraisemblablement »
auquel appartient « vraisemblablement » ![]() .
.
Soit ![]() une fonction de
une fonction de ![]() vers
vers ![]() . On dit que
. On dit que ![]() est un intervalle de confiance de niveau
est un intervalle de confiance de niveau ![]() si et seulement si
si et seulement si ![]()
Exemple : le modèle de Bernouilli:
On a vu au chapitre convergence que pour la loi de Bernouilli de paramètre ![]() .
.
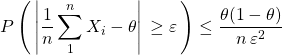
et la max de la fonction ![]() sur
sur ![]() est
est ![]() donc :
donc :
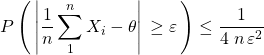
En posant ![]() ,
, ![]() et
et ![]() définissent un intervalle de confiance
définissent un intervalle de confiance
(par excès) de niveau ![]()
Exemple 17
On considère un sondage dans lequel deux réponses sont possibles, « oui » et « non ».
Combien faut-il interroger de personnes pour avoir une estimation à 0.03 près du pourcentage de gens en faveur de « oui », et ce au moins 19 fois sur 20.
Soit ![]() la proportion de la population totale favorable au “oui”. Quand on interroge n personnes prises au hasard, indépendamment, comme c’est le cas dans les sondages, en notant 1 lorsque la réponse est « oui » et 0 lorsque la réponse est « non », on observe
la proportion de la population totale favorable au “oui”. Quand on interroge n personnes prises au hasard, indépendamment, comme c’est le cas dans les sondages, en notant 1 lorsque la réponse est « oui » et 0 lorsque la réponse est « non », on observe ![]() variables aléatoires indépendantes de loi
variables aléatoires indépendantes de loi ![]() .
.
![]()
ici on fixe ![]() et on veut
et on veut ![]() , soit
, soit ![]()
![]() Le modèle gaussien
Le modèle gaussien
Considérons un échantillon gaussien ![]() ,Autrement dit
,Autrement dit ![]() sont des variables aléatoires indépendantes de loi
sont des variables aléatoires indépendantes de loi ![]() .
.
Les estimateurs ![]() et
et ![]() introduits plus hauts possèdent des propriétés très précises:
introduits plus hauts possèdent des propriétés très précises:
(1) ![]() suit une loi
suit une loi ![]() ou
ou ![]() suit une loi
suit une loi ![]()
(2) ![]() suit une loi du chi-deux à
suit une loi du chi-deux à ![]() degrés de liberté .
degrés de liberté .
(3) ![]() et
et ![]() sont indépendantes.
sont indépendantes.
(4) ![]() suit une loi de Student à
suit une loi de Student à ![]() degrés de liberté.
degrés de liberté.
La démonstration du point (2) est assez délicate, le point (4) est évident en remarquant que:
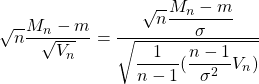
Exemple d’utilisation :
![]() Intervalle de confiance pour
Intervalle de confiance pour ![]() lorsque
lorsque ![]() est connu: Comme
est connu: Comme ![]() suit une loi
suit une loi ![]()
Fixons un niveau de confiance 0 < ![]() < 1. et soit
< 1. et soit ![]() tel que
tel que ![]() , par symétrie de la courbe de densité, on obtient
, par symétrie de la courbe de densité, on obtient ![]() ainsi
ainsi ![]()
…et nous venons de construire un intervalle de confiance de niveau ![]() pour
pour ![]() .
.
![]() Intervalle de confiance pour m lorsque
Intervalle de confiance pour m lorsque ![]() est inconnu:
est inconnu: ![]() suit une loi de Student à
suit une loi de Student à ![]() degrés de liberté, on cherche dans la table le nombre
degrés de liberté, on cherche dans la table le nombre ![]() tel que
tel que ![]() , par symétrie de la courbe de densité, on obtient
, par symétrie de la courbe de densité, on obtient ![]() et on construit l’intervalle de confiance comme ci-dessus.
et on construit l’intervalle de confiance comme ci-dessus.
Exemple 18
On suppose que le taux de cholestérol X d’un individu choisi au hasard dans une population donnée suit une loi normale. Sur un échantillon de 100 individus, on constate la moyenne des taux observés est 1.55 (gr pour mille). On constate aussi une variance corrigée![]()
Donner un intervalle de confiance pour la moyenne ![]() au niveau de confiance 0.95.
au niveau de confiance 0.95.
![]() suit une loi de Student à
suit une loi de Student à ![]() degrés de liberté, on cherche dans la table le nombre
degrés de liberté, on cherche dans la table le nombre ![]() tel que
tel que ![]() .
.
On lit ![]() .
.
![]()
Soit ![]() , au niveau de confiance 0.95
, au niveau de confiance 0.95
![]() Comparaison de deux moyennes :
Comparaison de deux moyennes :
On considère deux populations sur lesquelles sont définies deux caractères numériques ![]() et
et ![]() distribués selon des lois de moyennes
distribués selon des lois de moyennes ![]() et
et ![]() et de même variance
et de même variance ![]() (inconnue).
(inconnue).
On souhaite tester s’il y a une différence significative entre les moyennes des deux populations. L’hypothèse nulle à tester est![]()
On dispose d’un échantillon de taille ![]() pour
pour ![]() et de taille
et de taille ![]() pour
pour ![]() .
.
![]() et soit
et soit ![]()
On considère 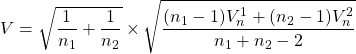
Alors la statistique ![]() suit une loi de Student à
suit une loi de Student à ![]() degrés de liberté.
degrés de liberté.
Exemple 19
De deux échantillons (mâles vs. femelles) de Souris des Cactus , dont on a mesuré le poids (g) chez l’individu adulte
F : (31, 25, 29, 30, 31, 28, 31, 29, 29, 33, 30, 28)
M : (28, 29, 30, 29, 27, 26, 27, 28, 25, 28)
Peut-on déceler, avec un risque d’erreur ![]() de
de ![]() , une différence de la moyenne du poids (g) chez l’individu adulte entre mâles et femelles ?
, une différence de la moyenne du poids (g) chez l’individu adulte entre mâles et femelles ?
![]() ,
, ![]()
![]() ,
, ![]()
On obtient ainsi ![]()
On cherche dans la table le nombre ![]() tel que
tel que ![]() , on lit
, on lit ![]()
![]() , on rejettera
, on rejettera ![]() , la différence des moyennes est significative.
, la différence des moyennes est significative.
![]() L’idée est maintenant de mélanger les résultats de la section convergence et les résultats ci-dessus pour obtenir des Intervalles de confiance asymptotiques:
L’idée est maintenant de mélanger les résultats de la section convergence et les résultats ci-dessus pour obtenir des Intervalles de confiance asymptotiques:
On dit que ![]() est un intervalle de confiance asymptotique de niveau
est un intervalle de confiance asymptotique de niveau ![]() si et seulement si:
si et seulement si:
![]()
Considérons une suite de variables aléatoires indépendantes et identiquement distribuées ![]() tel que
tel que ![]() et
et ![]() .
.
Soit l’estimateur ![]() ,d’après le T.C.L.,
,d’après le T.C.L., ![]()
![]() et l’estimateur
et l’estimateur ![]()
on en déduit:
![]()
Soit ![]() définit comme dans l’exemple précédent, l’intervalle
définit comme dans l’exemple précédent, l’intervalle ![]() est un intervalle de confiance asymptotique de niveau
est un intervalle de confiance asymptotique de niveau ![]() pour estimer
pour estimer ![]()
Exemple 19
On veut estimer la taille moyenne des hommes adultes dans une population. Un échantillon de 100 individus a donné les résultats suivants :
![]() et
et ![]()
Donner un intervalle de confiance à ![]() pour la taille moyenne de la population.
pour la taille moyenne de la population.
Soit ![]() tel que
tel que ![]() soit
soit ![]() .
. ![]() (voir table)
(voir table)
et l’intervalle ![]() est l’intervalle cherché.
est l’intervalle cherché.
Dans le cas particulier du modèle de bernoulli, ![]() et le résultat de convergence s’écrit:
et le résultat de convergence s’écrit:
![]()
Et l’intervalle ![]() est un intervalle de confiance asymptotique de niveau
est un intervalle de confiance asymptotique de niveau ![]() pour estimer
pour estimer ![]() , et comme
, et comme ![]() on utilise généralement l’intervalle
on utilise généralement l’intervalle ![]()
Exemple 20
Reprenons l’exemple 17 , on sait que pour ![]() ,
, ![]() Soit le
Soit le ![]() demandé.
demandé.
On souhaite ![]() donc
donc ![]()
Cette estimation est plus précise pour de grandes valeurs de ![]() (on a déjà vu que l’inégalité de Tchebychev n’était pas de très grande qualité.
(on a déjà vu que l’inégalité de Tchebychev n’était pas de très grande qualité.
Bonus: le test de corrélation de Pearson
Rappel, on appelle coefficient de corrélation entre deux variables ![]() et
et ![]() le nombre
le nombre ![]() , si
, si ![]() , il existe une relation affine entre ces deux variables.
, il existe une relation affine entre ces deux variables.
Un coefficient proche de 1 est un indice reflétant une relation linéaire entre deux variables continues.
On veut donc savoir si, dans la population ces deux variables sont réellement corrélées ou pas. On doit donc réaliser un test d’hypothèse.
On choisit ![]() : Pas de corrélation entre les deux variables :
: Pas de corrélation entre les deux variables :![]()
On choisit de travailler avec l’estimateur ![]()
![]() suit, sous
suit, sous ![]() , une loi de Student à
, une loi de Student à ![]() degrés de liberté, là encore les calculs permettant de démontrer ce résultat sont très pénibles.
degrés de liberté, là encore les calculs permettant de démontrer ce résultat sont très pénibles.
Exemple 21
Pour illustrer ce type de problème, nous aimerions savoir si le poids influence le taux de glycémie. Le poids et le taux de glycémie de 20 adultes ont été récoltés. Voici les données obtenues:
![]()
dans cette situation ![]() et donc la valeur de
et donc la valeur de ![]() observée est
observée est ![]()
On cherche dans la table le nombre ![]() tel que
tel que ![]() .
.
On lit ![]() ,
,
![]() donc on ne rejette pas
donc on ne rejette pas ![]() .
.
Il ne semble pas y avoir de relation de type linéaire entre poids et glycémie.
Annexe1
Compléments sur les fonctions caractéristiques d’une variable aléatoire ![]() :
: ![]()
![]() Si X suit une loi exponentielle de paramètre
Si X suit une loi exponentielle de paramètre ![]() :
:
![]()
![]() Si
Si ![]() suit une loi
suit une loi ![]() :
:
![]()
donc ![]()
ce qui , à l’aide d’une intégration par partie donne : ![]() , or la solution de l’équation différentielle
, or la solution de l’équation différentielle ![]() a pour solution
a pour solution ![]() et comme
et comme ![]() , on en déduit
, on en déduit ![]() .
.
![]() Si
Si ![]() suit une loi Gamma de paramètres
suit une loi Gamma de paramètres ![]() et
et ![]() , notée
, notée ![]() , alors la densité de
, alors la densité de ![]() est la fonction définie sur
est la fonction définie sur ![]() par
par ![]()
où ![]() est la fonction définie par
est la fonction définie par ![]()
![]()
![]()
ce qui , à l’aide d’une intégration par partie donne : ![]() , or la solution de l’équation différentielle
, or la solution de l’équation différentielle ![]() a pour solution
a pour solution ![]() et comme
et comme ![]() , on en déduit
, on en déduit ![]() .
.
Remarques :
– Pour ![]() , on retrouve bien la fonction caractéristique d’une loi exponentielle .
, on retrouve bien la fonction caractéristique d’une loi exponentielle .
-La somme de ![]() variables aléatoires de même loi exponentielle de paramètre
variables aléatoires de même loi exponentielle de paramètre ![]() est une loi Gamma de paramètres (
est une loi Gamma de paramètres (![]() ,
, ![]() ).
).
-La somme de deux variables aléatoires indépendantes de lois Gamma de paramètres respectifs (![]() ,
, ![]() ) et (
) et (![]() ,
, ![]() ) a pour loi une loi Gamma de paramètres (
) a pour loi une loi Gamma de paramètres (![]() ,
, ![]() ).
).
Si ![]() suit une loi
suit une loi ![]() , déterminons la fonction caractéristique de
, déterminons la fonction caractéristique de ![]() :
:
![]()
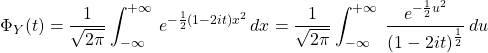 , en posant
, en posant ![]()
Soit 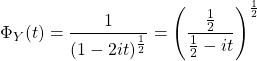 ….soit la fonction caractéristique d’une loi Gamma de paramètres (
….soit la fonction caractéristique d’une loi Gamma de paramètres (![]() ,
, ![]() ).
).
![]() On en déduit que si
On en déduit que si ![]() sont des variable aléatoires indépendantes qui suivent la loi normale
sont des variable aléatoires indépendantes qui suivent la loi normale ![]() alors
alors ![]() suit une loi Gamma de paramètres (
suit une loi Gamma de paramètres (![]() ,
, ![]() ) ce qui correspond à une loi du khi-deux à
) ce qui correspond à une loi du khi-deux à ![]() degrés de liberté.
degrés de liberté.