géométrie projective, exemple de calculs(2)

$\bullet$ Soit $D$ une droite affine d’équation $f$ et soient a, b deux points distincts du plan affine. On suppose que $D$ coupe (ab) en m. On a les propriétés suivantes :

1) On a $m =\dfrac{f(b)a - f(a)b}{f(b) - f(a)}$ .

2) On a la formule : $\dfrac{\overline{ma}}{\overline{mb}}=\dfrac{f(a)T(b)}{f(b)T(a)}$

$\bullet$ $\underline{\text{Théorème}\; \text{de}\; \text{Thalès}}$

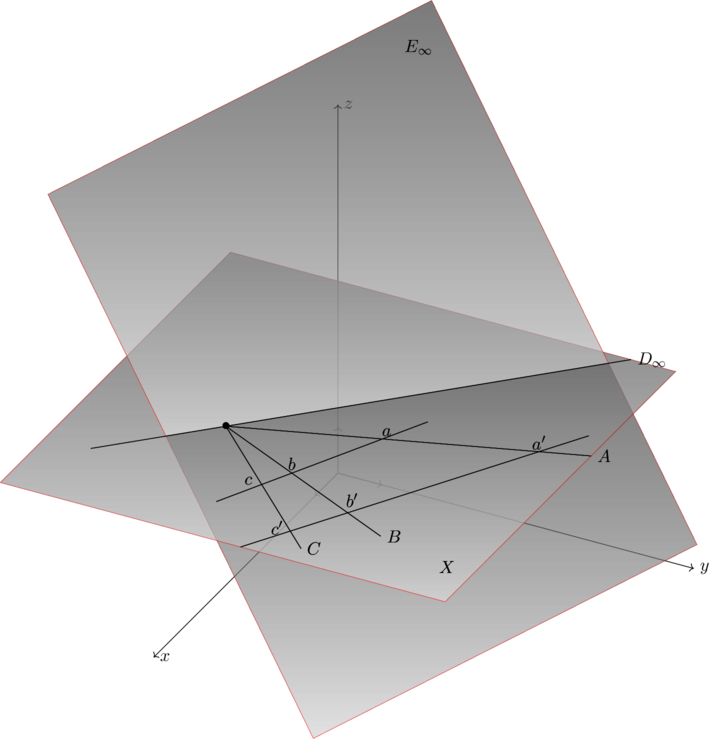
Soient A,B,C trois droites parallèles. Deux droites $D$ , $D'$ coupent respectivement A,B,C en $a, b, c ; a', b', c'$ .

On a la formule : $\dfrac{\overline{ab}}{\overline{ac}}=\dfrac{\overline{a'b'}}{\overline{a'c'}}$

En effet, soit f une équation de A, on a:
$\dfrac{\overline{ab}}{\overline{ac}}=\dfrac{f(b)T(c)}{f(c)T(b)}$ et $\dfrac{\overline{a'b'}}{\overline{a'c'}} =\dfrac{f(b')T(c')}{f(c')T(b')}$ . Mais, comme $B = (bb')$ est parallèle à A on a $f(b)T(b') =f(b')T(b)$ et de même, $f(c)T(c') = f(c')T(b)$ .
Le résultat s’ensuit.

Exemple, situation 1, (T=x+y+z).

Rendered by QuickLaTeX.com

$A$ : $3x+y-z=0$

$B$ : $2x-y-4z=0$

$C$ : $x-y-3z=0$

Commençons par montrer que $A$ et $B$ sont bien parallèles, en calculant $T(f \wedge g) = 0$ , avec $f$ et $g$ équations respectives de $A$ et $B$ .

$T(f \wedge g) =$

$T(1\times(-4)-(-1)\times(-1),-(3\times(-4)-2\times(-1)), 3\times(-1)-2\times1)$

$=T(-5,10,-5)=T(1,-2,1)$ (ici on normalise les coordonnées du point obtenu, $z=1$ )

$=1-2-1=0$ !

Idem pour les droites $A$ et $C$ .

Les points $a$ , $b$ , $a'$ et $c'$ ont pour coordonnées respectives $(0,1,1)$ , $(2,0,1)$ , $(-1,4,1)$ , $(4,1,1)$

On obtient les coordonnée de $c$ et $b'$ grâce à la formule $c =\dfrac{f(b)a - f(a)b}{f(b) - f(a)}$ , où $f$ est ici l’équation de $C$ .

Soit $c =\dfrac{-a +4b}{3}= (\frac{8}{3},-\frac{1}{3},1)$ , on obtiendra de même, $b'= (\frac{37}{13},-\frac{22}{13},1)$

On obtient alors bien, avec $f$ équation de $A$ ,

$\dfrac{\overline{ab}}{\overline{ac}}=\dfrac{f(b)T(c)}{f(c)T(b)}=\dfrac{5\times \frac{10}{3}}{\frac{20}{3}\times 3}=\dfrac{5}{6}$

et $\dfrac{\overline{a'b'}}{\overline{a'c'}}=\dfrac{f(b')T(c')}{f(c')T(b')}=\dfrac{\frac{120}{13}\times 6}{12\times \frac{72}{13}}=\dfrac{5}{6}$ !

$\bullet$ On suppose $E_{\infty}$ muni d’une base $e_1$ , $e_2$ . Soit abc un triangle de X. La mesure de l’aire algébrique du triangle abc relativement à cette base est la moitié du déterminant des vecteurs $\overrightarrow{ab}$ et $\overrightarrow{ac}$ sur la base $e_1$ , $e_2$ ou plus simplement:

$\matbb{A}(abc) =\dfrac{[a,b,c]}{2 T(a)T(b)T(c) }$

Exemple, situation1 , (T: x+y+z=0)

Soient $a(0,1,1)$ , $b(2,0,1)$ et $c(3,3,1)$

$\overrightarrow{ab}=\dfrac{b}{T(b)}- \dfrac{a}{T(a)} =(\dfrac{2}{3},\dfrac{-1}{2},\dfrac{-1}{6})$

$\overrightarrow{ac}=\dfrac{c}{T(c)}- \dfrac{a}{T(a)} =(\dfrac{3}{7},\dfrac{-1}{14},\dfrac{-5}{14})$

Prenons $e_1(1,0,-1)$ et $e_2(0,1,-1)$ comme base de $E_{\infty}$ , les vecteurs ont alors pour coordonnées respectives $( \dfrac{2}{3} ,-\dfrac{1}{2} )$ et $( \dfrac{3}{7} ,-\dfrac{1}{14} )$ .

Avec la première formule : 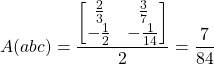$\matbb{A}(abc) =\dfrac{\begin{bmatrix} \frac{2}{3} & \frac{3}{7} \\ -\frac{1}{2} & -\frac{1}{14} \end{bmatrix} }{2}=\dfrac{7}{84}$

et la deuxième : 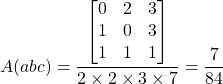$\matbb{A}(abc) =\dfrac{\begin{bmatrix} 0 & 2&3 \\ 1&0&3 \\ 1&1&1 \end{bmatrix} }{2\times 2\times 3\times 7}=\dfrac{7}{84}$ !

D’autres formules fondamentales :

$f\wedge (a \wedge b) =f(b)a-f(a)b$

$a \wedge (f \wedge g) =g(a)f-f(a)g$

$[a,b,f \wedge g] =f(a)g(b)-f(b)g(a) = [f,g,a \wedge b]$

$[a \wedge a',b \wedge b',c \wedge c'] = [a,a',c][b,b',c']-[a,a',c'][b,b',c]$

…ou encore $[a,b,c]d = [b,c,d]a + [c,a,d]b + [a,b,d]c$

$\bullet$ Si maintenant on munit $E^*$ d’une forme quadratique dégénérée telle que T est une base du noyau de cette forme. Cela
permet définir sur le plan affine X,
et sans aucune donnée supplémentaire, les notions de parallélisme et d’orthogonalitée, ainsi que la forme q sur $E_{\infty}$ en posant $q(n_f)=q^*(f)$ et la forme polaire $\phi$ de $q$ appelée produit scalaire.
On définit alors avec des points normalisés $q(\overrightarrow{ab})=q(b-a)$
et $\phi(\overrightarrow{ab},\overrightarrow{ac})= \phi(b-a,c-a)$

On parlera de $\underline{ \text{plan}\; \text{affine}\; \text{euclidien}}$ lorsqu’on est dans cette situation.

$\sqrt{q(\overrightarrow{ab})}$ définit alors une distance.

Soient $\overline{A}$ et $\overline{B}$ deux droites affines, l’invariant $I^*(\overline{A},\overline{B})=\dfrac{\phi^*(A,B)^2}{q^*(A)q^*(B)}$ permet de définir la notion d’ $\underline{\text{angle}\; \text{non} \;\text{orienté}\; \text{de}\; \text{droites}}$ .

Si A, A’ sont parallèles et si B est sécante à A et A’, on a $I^*(\overline{A},\overline{B}) =I^*(\overline{A'},\overline{B})$ . C’est l’égalité des angles « alternes internes »

Un autre invariant de deux droites $\dfrac{[A,B,l]^2}{q^*(A)q^*(B)}$ correspond lui au sinus dans le cas réel et la formule de Lagrange: $q^*(A)q^*(B)=\phi^*(A,B)^2+\delta(q^*)[A,B,l]^2$ est la traduction de $\cos^2\theta+\sin^2\theta=1$ .

La formule des aires : $b \wedge c + c \wedge a + a \wedge b = [a, b, c]l$ permet alors d’obtenir la formule d’Al Kashi:
$q(\overrightarrow{bc})=q(\overrightarrow{ab})+q(\overrightarrow{ac})-2\phi(\overrightarrow{ab},\overrightarrow{ac})$ , dont découle le théorème de Pythagore.

La quantité 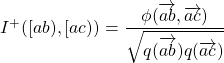$I^+([ab),[ac))=\dfrac{\phi(\overrightarrow{ab},\overrightarrow{ac})}{\sqrt{q(\overrightarrow{ab})q(\overrightarrow{ac})}}$ permet elle de définir la notion d’ $\underline{\text{angle}\; \text{non}\; \text{orienté}\; \text{de}\; \text{demi-droites}}$ : $\widehat{bac}=ArccosI^+([ab),[ac))$

On retrouve alors la formule familière: $\phi(\overrightarrow{ab},\overrightarrow{ac})=ab\; ac\; cos\;\widehat{bac}$

L’aire algébrique de $abc$ , $\dfrac{1}{2}\dfrac{[a,b,c]}{l(a)l(b)l(c)}$ , s’écrit alors: $\dfrac{1}{2}\;ab\;ac\;\sin\;\widehat{bac}$ .

Angles orientés de vecteurs:

Rappelons que le groupe $O^+(q)$ est isomorphe au groupe $\mathbb{R} / 2 \pi \mathbb{Z}$ par l’application qui à $\overline{\theta}$ associe la rotation vectorielle d’angle $\overline{\theta}$ , notée $\rho(\overline{\theta})$ .

Soient $v$ et $w$ deux vecteurs unitaires de $E_{\infty}$ . On appelle angle des vecteurs $v$ et $w$ et on note
$(v,w)$ l’unique élément $\overline{\theta} \in \mathbb{R} / 2 \pi \mathbb{Z}$ tel que $\rho(\overline{\theta})(v) = w$ .

On a alors les propriétés suivantes :

1) $(u,w) = (u, v) + (v,w)$ (relation de Chasles).

2) $(u,v) = (u', v') \Leftrightarrow (u, u') = (v, v')$ (règle du parallélogramme).

La relation de Chasles vaut pour des angles de sommets différents et cette propriété est constitutive de la géométrie euclidienne.

On appelle angle orienté des droites (ab) et (ac) et on note ((ab),(ac)) la classe modulo $\pi$ de l’angle de vecteurs $(\overrightarrow{ab},\overrightarrow{ac})$ .

Soient $A,B$ deux équations de droites normalisées et soient $a =l\wedge A$ et $b =l\wedge B$ les vecteurs unitaires associés. On a les formules $cos(a, b) =\phi^*(A,B)$ et $sin(a, b) =[A,B, l]$ .

la formule suivante:

$[A;B; l][A;C; l] =\left|\begin{array}{cl}q^*(A)& \phi^*(A,C)\\\phi^*(B,A)&\phi^*(B,C)\\\end{array}\right|.$

correspond alors à la relation: $\cos(\beta +\gamma) = \cos \beta \cos\gamma - \sin \beta \sin \gamma$

MATHEMATIQUES

géométrie projective, exemple de calculs(2)

Une journée sans Maths …