Ci-dessous un petit résumé en image des deux premières parties du livre de géométrie projective de Daniel Perrin ( lien ici: Géométrie ) Vous trouverez dans un article du même nom un petit résumé écrit.


Démonstration :![]()
![]()
Une lecture affine de cette relation donne une condition universelle de parallélisme ou de concours:

(AA’), (BB’) et (CC’) sont concourantes si et seulement si: Aire(BB’C).Aire (AA’C’)= Aire(B’BC’).Aire(A’AC)

Démonstration: ![]()

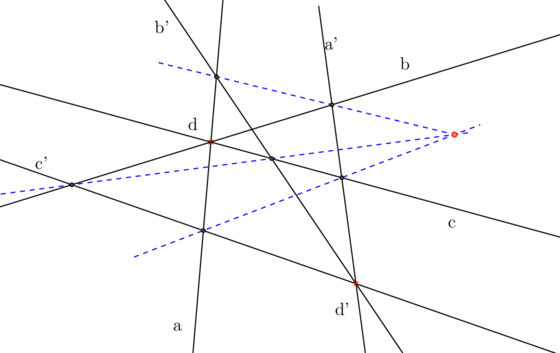
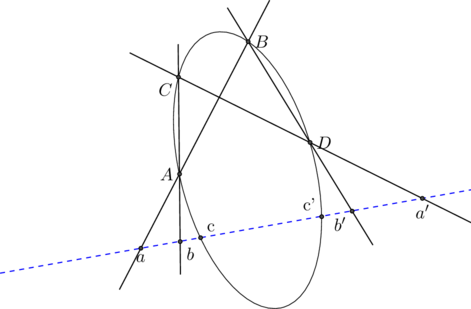
L’involution qui échange a et a’ et b et b’ échange aussi c et c’ que la conique soit dégénérée ( AD ![]() BC)…ou non !
BC)…ou non !

Remarque :![]()

[B,C, a,a’].[C,A,b,b’].[A,B,c,c’]=1 et avec d’ à l’infini……..
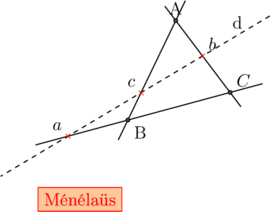
![]()
La relation fondamentale [b, c, d]a + [c, a, d]b + [a, b, d]c = [a, b, c]d (![]() ), donne le théorème de Gergonne projectif:
), donne le théorème de Gergonne projectif:
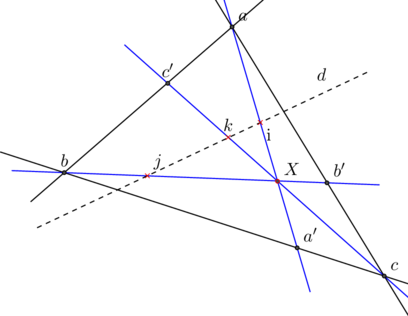
[X,a,a’,i].[X,b,b’,j].[X,c,c’,k]= 1
Ce qui, avec ![]() à l’infini donne le théorème de Gergonne affine:
à l’infini donne le théorème de Gergonne affine:
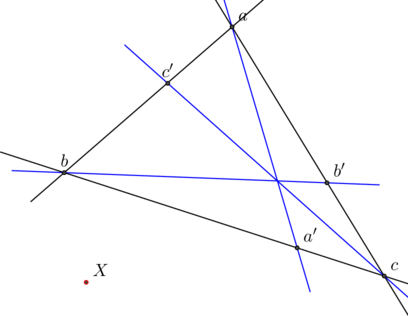
![]()
La relation : [a, b, c] [f, g, h] = f(a)g(b)h(c) + f(b)g(c)h(a) + f(c)g(a)h(b)
-f(c)g(b)h(a) – f(b)g(a)h(c) – f(a)g(c)h(b) donne au choix:
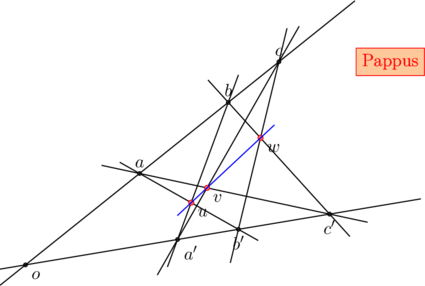
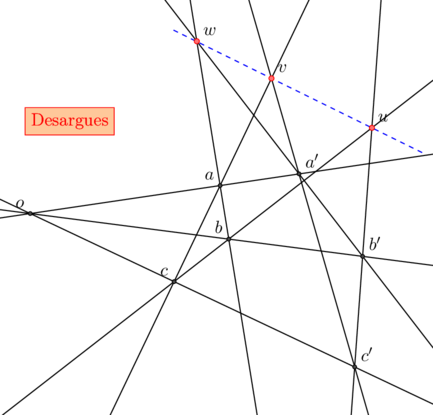
![]() (bb’) , (cc’) et (aa’) sont concourantes si et seulement si les points u , v et w sont alignés
(bb’) , (cc’) et (aa’) sont concourantes si et seulement si les points u , v et w sont alignés
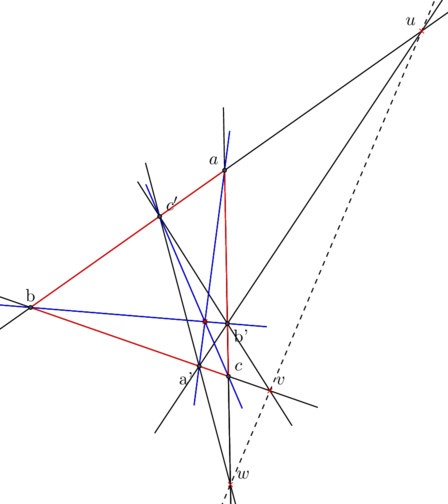
ou encore mieux…
![]() (bb’) , (cc’) et (aa’) sont concourantes si et seulement si [u,v,w,k].[v,w,u,i].[w,u,v,j] = -1
(bb’) , (cc’) et (aa’) sont concourantes si et seulement si [u,v,w,k].[v,w,u,i].[w,u,v,j] = -1
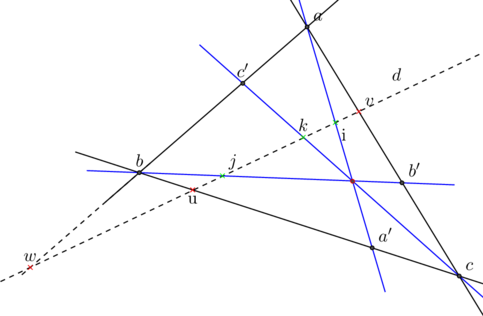
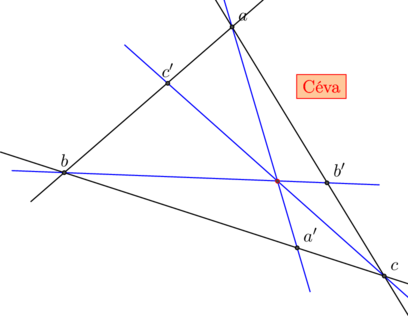
Ce qui en envoyant d à l’infini donne le théorème de Céva usuel : ![]()
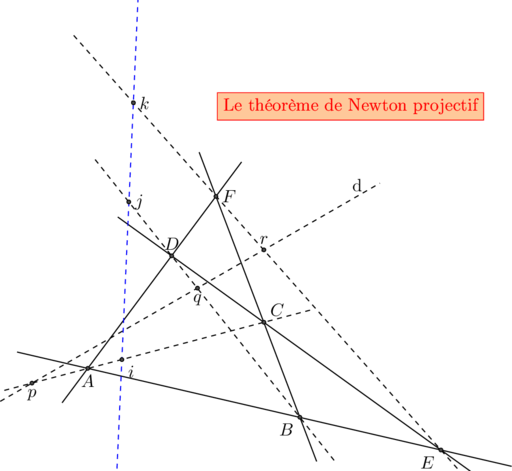
Les conjugués harmoniques de p , q et r par rapport à A,C , B,D et E,F sont alignés.
….et avec d à l’infini…

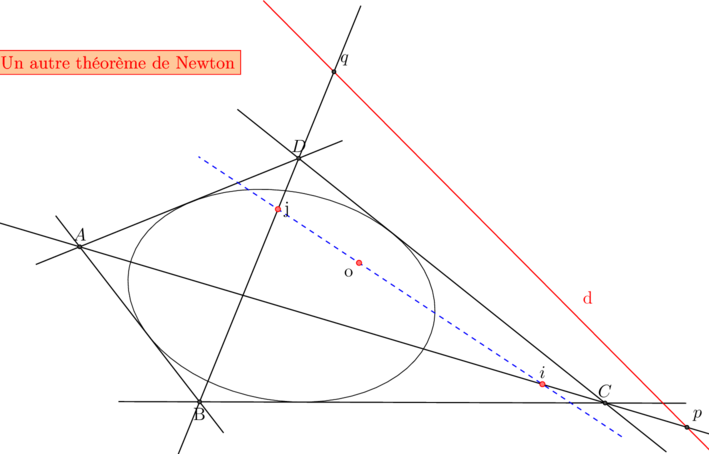
Soit o un point et d sa polaire, les conjugués harmoniques de p et q par rapport à A et C et B et D sont alignés avec o.