Solutions exercices de probabilité.

Exercice 1:
Nombre de cas favorables 5
Nombre de cas total: Autant qu’il y a de « mot » semblables
à « lccllcc » où « l » représente un livre et « c » les cloisons séparant les tiroirs. 3 livres , 4 cloisons , soit « 3 parmi 7 » cas possibles : 35 d’où le résultat : $\dfrac{1}{7}$

Exercice 2:
Comme B joue en premier, déterminons la probabilité pour que B gagne:
Soit B gagne le premier tour soit il gagne plus tard, c’est à dire après avoir perdu le premier tour puis après que A a lui aussi perdu sa première tentative, notons que nous sommes alors revenu dans les conditions initiales, ce qui se traduit par:
$P(B)=\dfrac{5}{36}+\dfrac{31}{36}\times\dfrac{30}{36}\times P(B)$
soit $P(B)=\dfrac{30}{61}$ et $P(A)=\dfrac{31}{61}$ .

Exercice 3:
Ici encore , soit B gagne le premier tour, soit il gagne plus tard, c’est à dire après qu’il y a eut égalité au premier tour. Comme les nombres de Pile des deux joueurs suivent respectivement des lois Binomiales de paramètres $(2,\frac{1}{2})$ et $(3,\frac{1}{2})$ , on obtient:
$P(B)=\dfrac{1}{2}+\dfrac{5}{16}\timesP(B)$
soit $P(B)=\dfrac{8}{11}$ .

Exercice 4:
Notons $T_i$ l’événement « la clé est dans le tiroir $i$ « , on cherche:
$P_{\bar{T_1}\cap\bar{T_2}\cap\bar{T_3}\cap\bar{T_4}\cap\bar{T_5}\cap\bar{T_6}}(T_7)$
Mais $P(\bar{T_1}\cap\bar{T_2}\cap\bar{T_3}\cap\bar{T_4}\cap\bar{T_5}\cap\bar{T_6}\cap T_7) =P(T_7)=\dfrac{\frac{1}{3}}{7}=\dfrac{1}{21}$

Et $P(\bar{T_1}\cap\bar{T_2}\cap\bar{T_3}\cap\bar{T_4}\cap\bar{T_5}\cap\bar{T_6})$
$=1-P(T_1\cup T_2\cup T_3\cup T_4\cup T_5\cup T_6)$
$=1-6\times \dfrac{\frac{1}{3}}{7}$

d’où le résultat : $\dfrac{1}{15}$

Exercice 5:

On note $S$ l’événement « trafic saturé » et $A_S$ l’événement « radio A annonce un trafic saturé ».
On cherche alors $p=P_{A_{\bar{S}}\cap B_S}(S)$ sachant que :
$P_S(A_{\bar{S}})=\frac{5}{100}$ et $P_S(B_S)=\frac{90}{100}$ .

$p=\dfrac{P(S\cap A_{\bar{S}}\cap B_S)}{P(S\cap A_{\bar{S}}\cap B_S)+P(\bar{S}\cap A_{\bar{S}}\cap B_S)}$

et comme $P(S\cap A_{\bar{S}}\cap B_S)=p(S) \times P_S(B_S)\times P_S(A_{\bar{S}})$
on obtient finalement:
$p=\dfrac{\frac{7}{10}\times \frac{90}{10} \times \frac{5}{100}}{\frac{7}{10} \times \frac{90}{10} \times \frac{5}{100}+\frac{3}{10} \times \frac{10}{10} \times \frac{95}{100}}=\dfrac{21}{40}$ … mieux vaut prendre le métro !

Exercice 6:

Exercice 7:
Il y a $\left(\begin{array}{c} n\\ 3\\ \end{array}\right)$ façons de choisir les emplacements réservés à ces trois boules , une seule manière de les affecter dans ces trois emplacements réservés, puis $(n-3)!$ façon de compléter le tirage.
On obtient alors 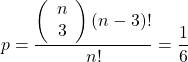$p=\dfrac{\left(\begin{array}{c} n\\ 3\\ \end{array}\right) (n-3)!}{n!}=\dfrac{1}{6}$

Exercice 8:
On note $R_i$ , $B_i$ et $V_i$ les événements « obtenir rouge ,bleu ou
vert au $i^{i\text{è}me}$ tirage ».
On cherche alors : $p=P(R_1\cap R_3)+P( B_1\cap B_3)+P(V_1\cap V_3))$
Or $P(R_1\cap R_3)=P(R_1\cap R_2 \cap R_3)+P(R_1\cap B_2 \cap R_3)+P(R_1\cap V_2 \cap R_3)$
Puis $P(R_1\cap R_2 \cap R_3)=P(R_1)\times P_{R_1}(R_2)\times P_{R_1\cap R_2}[(R_3)$ ..et ainsi de suite .
Soit $P(R_1\cap R_3)=\dfrac{10}{1000}$ , $P(B_1\cap B_3)=\dfrac{108}{1000}$ et $P(V_1\cap V_3)=\dfrac{305}{1000}$
Soit finalement $p=\dfrac{423}{1000}$

Exercice 11:
Supposons que A gagne la première partie:
« si A perd, il se retrouve dans la même situation que B au tour précédent », donc: $p_A=\frac{1}{2} + \frac{1}{2}\times p_B$
« Si A perd, B se retrouve dans la même situation que C au tour précédent »,donc: $p_B=\frac{1}{2}\times p_C$
et de même , on aura : $p_C=\frac{1}{2}\times p_A$
Finalement $p_C=\dfrac{2}{7}$ est la seule valeur certaine et on en déduit:

$p_A=p_B=\dfrac{1-\frac{2}{7}}{2}=\dfrac{5}{14}$

les joueurs qui commencent la partie sont avantagés !

Exercice 12:
Supposons que la tige soit divisée en $2m$ parties égales et appelons $x$ , $y$ et $z$ la longueur des trois morceaux obtenus. On aura :
$x+y+z=2m$

et pour que la construction du triangle soit envisageable:
$x\leq y+z$ , $y\leq z+x$ et $z\leq x+y$ ce qui se résume à:
$x\leq m$ , $y\leq m$ et $x+y\geq m$

Déterminons maintenant le nombre de cas favorables:
si $x=0$ alors $y=m$
si $x=1$ alors $y=m,m-1$
si $x=2$ alors $y=m,m-1,m-2$
……………………………
si $x=m$ alors $y=m,m-1m-2, m-3, ...,0$

Soit $1+2+3+4+..+m+1=\dfrac{(m+1)(m+2)}{2}$ cas favorables.

…et le nombre de cas possibles:
si $x=0$ alors $y=2m,2m-1,2m-2,2m-3,...,2,1,0$
si $x=1$ alors $y=2m-1,2m-2,2m-3,...,2,1,0$
si $x=2$ alors $y=2m-2,2m-3,...,2,1,0$
……………………………..
si $x=2m$ alors $y=0$

Soit $1+2+3+4+..+2m+1=\dfrac{(2m+1)(2m+2)}{2}$ cas possibles.

Le rapport entre ces deux nombres est $\dfrac{m+2}{2(2m+1)}$ qui tend lorsque $m$ tend vers $+\infty$ vers $\dfrac{1}{4}$ qui est la probabilité cherchée.

MATHEMATIQUES

Solutions exercices de probabilité.

Une journée sans Maths …