Birapport (partie 1) | MATHEMATIQUES

Birapport de quatre points:

Définition:

Soit $D$ une droite projective et soient $a,b,c,d$ quatre points de $D$ , avec $a,b,c$ distincts.
Soit $h$ l’unique homographie de $D$ sur $P^1(k)$ définie par $h(a) = \infty, h(b) = 0, h(c) = 1$ .
On appelle birapport des quatre points $a,b,c,d$ pris dans cet ordre l’élément $h(d) \in P^1(k) = k \cup {\infty}$ et on le note [a,b,c,d].
Soit $f : d \rightarrow d'$ une homographie. On a l’égalité :
$[a,b,c,d] = [f(a), f(b), f(c), f(d)]$ .

Les perspectives seront par la suite des homographies particulièrement utilisées ainsi que les incidences : Soit $D$ une droite et $m$ un point n’appartenant pas à $D$ . On appelle incidence l’ application qui à toute droite $\delta$ passant par $m$ associe l’unique point d’intersection $x$ de $D$ et $\delta$ .

Calcul du birapport:

Soit $D$ une droite projective et soient $a,b,c,d$ quatre points de $D$ , avec $a,b,c$ distincts, on a la formule suivante:

$\bullet$ $[a,b,c,d]=\dfrac{\overline{ac}}{\overline{ad}}\div\dfrac{\overline{bc}}{\overline{bd}}$ = r

$\bullet$ $[b,a,c,d] = [a,b,d,c] =\dfrac{1}{r}$

$\bullet$ $[a,c,b,d] = 1 - r$ ( $\maltese$ )

$\bullet$ Soient $a, b, c, d, e$ cinq points distincts d’une droite projective $D$ . On a la formule : $[b, c, d, e] \times [c, a, d, e] \times [a, b, d, e] = 1$ .

Exemple: $a$ , $c$ et $d$ étant fixés, pour construire $b$ tel que $[a,b,c,d]=$ r . Sur un droite quelconque, on placera $e$ et $f$ tels que $\dfrac{af}{ae}=$ r. La parallèle à $(ef)$ passant par le point d’intersection de $(cf)$ et $(de)$ permet d’obtenir le point cherché.

Rendered by QuickLaTeX.com

Pour la démonstration de $(\maltese)$ , on considère les homographies $f(z) =1-z$ et $h$ telle que $h(d)=r$ .

Soit $u=f \circ h$ , on a bien $u(a) = \infty$ , $u(c) = 0$ , $u(b) = 1$ et alors $u(d)=1-r$

Remarquons au passage que la relation ( $\maltese$ ) traduit la relation fondamentale ( ou « grosse relation de Chasles »):

$\overline{ab}.\overline{cd}+\overline{ac}.\overline{db}+\overline{ad}.\overline{bc}=0$

…vérifiée pour quatre points quelconques $a$ , $b$ , $c$ et $d$ d’une droite quelconque.

Soit $m$ un point quelconque de la droite $D$ , on a alors :

$[a,b,c,d]=\dfrac{\dfrac{\overline{mb}}{\overline{ab}}-\dfrac{\overline{md}}{\overline{ad}}}{\dfrac{\overline{mb}}{\overline{ab}}-\dfrac{\overline{mc}}{\overline{ac}}}$

En effet $[a,b,c,d] = [d,c,b,a] =(\dfrac{\overline{db}}{\overline{da}}\div\dfrac{\overline{mb}}{\overline{ma}})\div(\dfrac{\overline{cb}}{\overline{ca}}\div\dfrac{\overline{mb}}{\overline{ma}})$

et comme $\overline{ab}.\overline{dm}+\overline{ad}.\overline{mb}+\overline{am}.\overline{db}=0$

alors $\dfrac{\overline{db}.\overline{ma}}{\overline{da}.\overline{mb}}=1-\dfrac{\overline{ab}.\overline{md}}{\overline{da}.\overline{mb}}$ ……..

…avec $m$ = $\infty$ on obtient alors la relation suivante

$[a,b,c,d]=\dfrac{\dfrac{1}{\overline{ab}}-\dfrac{1}{\overline{ad}}}{\dfrac{1}{\overline{ab}}-\dfrac{1}{\overline{ac}}}$

Une premières propriété: ( $\mathcal{P}$ )

Soient $a,b,c,d$ quatre points de $D$ et $a',b',c',d'$ quatre points de $D'$ , si $[a,b,c,d]=[a',b',c',d']$ et $a=a'$ alors les droites $(bb')$ , $(cc')$ et $(dd')$ seront concourantes .

Rendered by QuickLaTeX.com

Ceci suffit pour démontrer le théorème de Pappus:
Soient $a$ , $b$ et $c$ trois points d’une droite $d_1$ et $a'$ , $b'$ et $c'$ trois points d’une droite $d_2$ , les trois points $(ab')\cap (a'b)$ , $(ac')\cap (a'c)$ et $(cb')\cap (c'b)$ seront alignés.

Rendered by QuickLaTeX.com

En effet $[aa',ab',ac',ac]=[ca',cb',cc',ca]$ donc $[a',m,x,b]=[y,n,c',b]$ et donc les droites $(a'y)$ , $(mn)$ et $(c'x)$ sont concourantes ce qui signifie que le point $(ac')\cap (a'c)$ se trouve sur $(mn)$ …

Ou le théorème suivant :

Soit $A,B,C,D$ un repère du plan projectif $P(E)$ et soit $\Delta$ une droite ne passant par aucun des points du repère. On note $a, b, c, a', b', c'$ les intersections de $\Delta$ avec les droites $(AC), (BD), (AB), (DC), (AD)$ et $(BC)$ respectivement et on suppose $a \neq a'$ . Alors, le birapport de quatre quelconque de ces points est égal à celui de leurs conjugués.

( Nous dirons plus loin que ces trois couples de points sont en involution).

Rendered by QuickLaTeX.com

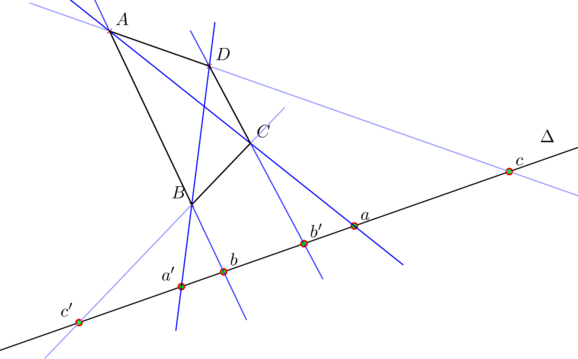
En effet on considère les perspectives $p_B$ de $\Delta$ sur $(AC)$ et $p_D$ de $(AC)$ sur $\Delta$ et leur composée $h$ qui est une homographie de $\Delta$ .
h(a’) = a’, h(b) = c’ et h(c) = b’, d’où l’égalité de birapports : $[a, a', b, c] = [a, a', c', b'] = [a', a, b', c]$ par permutation. Il en résulte qu’on a $[a, a', b, c] = [f(a), f(a'), f(b), c']$ d’où $c' = f(c)$ .

Somme et produit:

On cherche ici à construire un point $z$ tel que tel que $[a, b, c, z] = [a, b, c, x] + [a, b, c, y]$
Cette relation étant équivalente à la relation $[b, a, x, z] = 1 -[b, a, y, z] = [b, y, a, z]$ , Le point $z$ cherché est
construit comme indiqué sur la figure ci dessous.

Rendered by QuickLaTeX.com

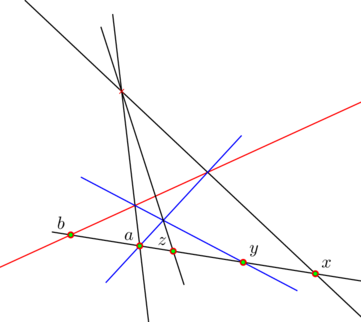
On cherche maintenant à construire un point $z$ tel que tel que $[a, b, c, z] = [a, b, c, x] \times [a, b, c, y]$ .
On a alors $[a, b, c, x] =[b, a, z, y]$ et le point $z$ cherché est construit à l’aide du théorème du Desargues.

Par un point $A$ on mène deux droites $(Aa)$ et $(Ay)$ puis une droite $\Delta$ passant par $b$ qui coupe $(Ay)$ en $D$ . $(Ac)$ coupe $\Delta$ en $C$ puis $(xC)$ recoupe $(Aa)$ en $B$ .

$(BD)$ recoupera $(ax)$ en $z$ qui est le point cherché.

Birapport de quatre droites:

Si $A,B,C,D$ sont quatre droites passant par $m$ , soit $\Delta$ une droite ne passant pas par $m$ et soient $a,b,c,d$ les traces de $A,B,C,D$ sur $\Delta$ .
Alors on a $[A,B,C,D]= [a,b,c,d]$ .
D’après la loi des sinus: $[A,B,C,D]=\dfrac{\sin(A,C)}{\sin(A,D)} \div \dfrac{\sin(B,C)}{\sin(B,D)}$

Rendered by QuickLaTeX.com

On a bien sur : $[a,b,c,d] =[a',b',c',d']$

Si $[A,B,C,D]=[A',B',C',D']$ et si $A=A'$ alors les points d’intersection de $B$ et $B'$ , $C$ et $C'$ et $D$ et $D'$ seront alignés.

Rendered by QuickLaTeX.com

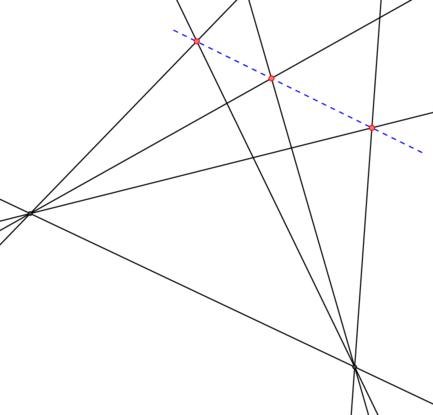
La propriété ci-dessus sera très utile pour résoudre le problème suivant: étant donné quatre points $a,b,c$ et $d$ d’une droite $d_1$ et étant donné trois points $a',b',c'$ d’une droite $d_2$ , trouver $d'$ tel que $[a,b,c,d]=[a',b',c',d']$ .

On utilisera deux points $O$ et $O'$ pris arbitrairement sur $(aa')$ et la propriété pour déterminer le point d’intersection de $(Od)$ et $(O'd')$ , donc le point $d'$ .

Énonçons au passage la version « duale » de la propriété ( $\mathcal{P}$ ) ci-dessus.
Soient $A,B,C,D$ quatre droites passant par $O$ et $A',B',C',D'$ quatre droites passant par $O'$ , si $[A,B,C,D]=[A',B',C',D']$ alors les droites $(A\cap B' A'\cap B)$ , $(A\cap C' A'\cap C)$ et $(B\cap C' B'\cap C)$ ….. seront concourantes .

Rendered by QuickLaTeX.com

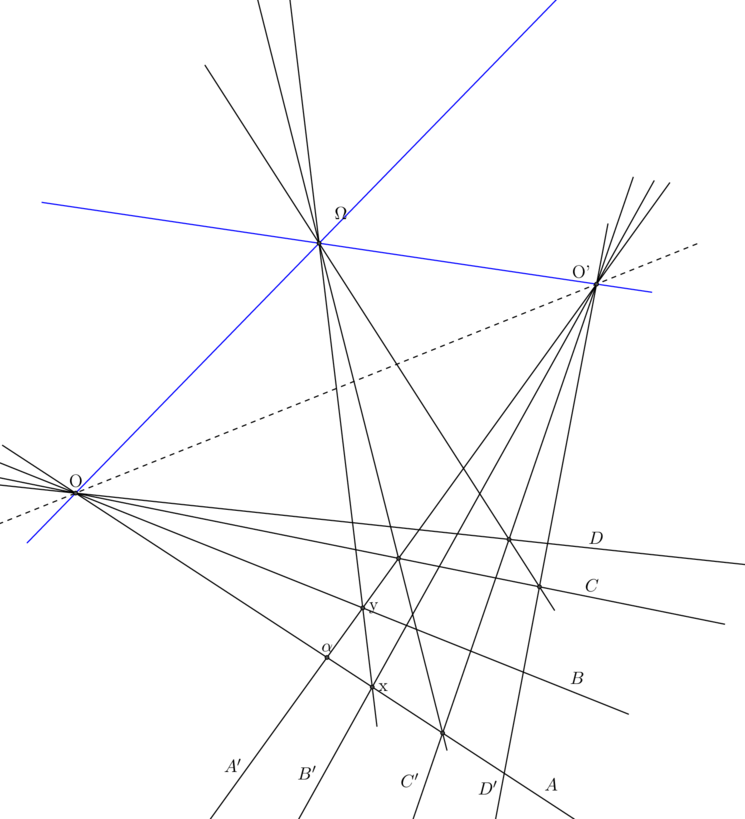
En effet, notons $x=A\cap B'$ et $y= A'\cap B$ et soient $E$ la droite du premier faisceau correspondant à $(OO')$ et $E'$ la droite du second correspondant à $(OO')$ .
$\omega =E\cap A'$ et $\omega ' =E' \cap A$
On considère $\Omega= E\cap E'$ on a alors $[A,B,(OO'),E]=[A',B',E',(OO')]$ , en considérant les intersections respectives par les droites $A'$ et $A$ , on obtient
$[\alpha,y,O',\omega]=[\alpha,x,\omega ', O]$
Donc

Revenons quelques instants sur la relation ( $\maltese$ ) ci-dessus qui permet de démontrer quelques beaux résultats:

$\bullet$ Elle peut s’écrire d’après la remarque ci-dessus :

$\sin(A,B)\sin(C,D)+\sin(A,C)\sin(D,B)+\sin(A,D)\sin(B,C)=0$

Si les quatre droites sont issues du centre du cercle unité, les arcs ab, cd, etc., mesurent alors les angles de ces droites.

Dans le cas particulier où bd= $\frac{\pi}{2}$ , $\sin(db)=-1$ , $\sin(ad)=\cos(ab)$ et $\sin(cd)=\cos(cb)=\cos(bc)$ et l’équation ci-dessus correspond à la formule bien connue:

$\sin(ab+bc)=\sin(ab).\cos(bc)+\sin(bc).\cos(ab)$

Rendered by QuickLaTeX.com

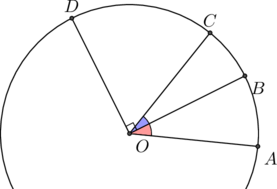
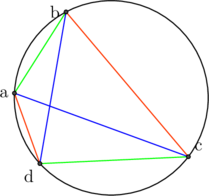
$\bullet$ Le théorème de Ptolémé:

Soit un quadrilatère $abcd$ inscrit dans un cercle, la relation
$\sin \frac{1}{2}ac.\sin\frac{1}{2}db=\sin\frac{1}{2}ab.\sin\frac{1}{2}cd+\sin\frac{1}{2}ad.\sin\frac{1}{2}ac$ obtenue en considérant les quatre points $a,b,c,d$ comme appartenant à quatre droites issues d’un cinquième point du cercle et le fait que ces sinus sont les demi-cordes $ab$ $cd$ , … donne:

$ac.db=ab.cd+ad.bc$

Rendered by QuickLaTeX.com

Une journée sans Maths …