Pour commencer deux petits lemmes sur les aires :
Soient 
et 
deux triangles tels que 
et 
soient parallèles, alors 
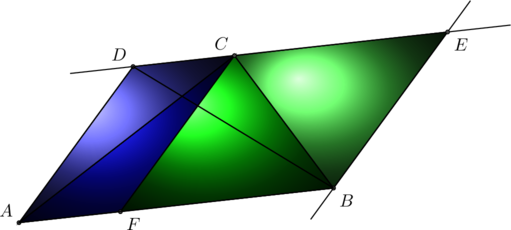
On trace les parrallèles à et 
, elles se coupent en 
, et l’aire de chaque triangle est égale à la moitié de celle du parallèlogramme 
.
Soit un triangle, 
un point de 
et 
un point de 
, alors 
…. 
pour les mêmes raisons… 
par différence (chevron)
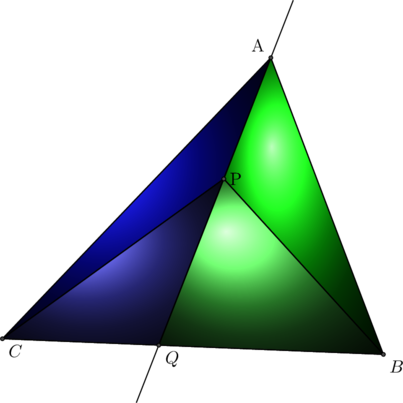
On utilise le fait que ces triangles ont le même hauteur.
Ceci suffit pour démontrer le théorème de Thalès :
Soit 
un triangle, 
et 
deux points de 
et 
, si 
et sont parallèles alors 
En effet,
donc en soustrayant à l’aire totale 
puis 
!
…ou le théorème de Ménélaus
X ,Y et Z étant trois points de 
, 
et , ces points sont alignés si et seulement si 
En effet :
, 
( chevron !) et 
Le théorème de Céva se démontre aussi facilement :X ,Y et Z étant trois points de , et , les droites 
, 
et 
sont concourantes si et seulement si 
En effet :
, 
et 
( chevron et rechevron et ..)
To be continued…