LE THÉORÈME DE CÉVA. | MATHEMATIQUES

Ci dessous , vous trouverez différentes façons de démontrer le théorème de Céva ainsi que quelques applications évidentes

Le théorème de Céva :

a ,b et c étant trois points de $(BC)$ , $(AC)$ et $(AB)$ , les droites $(Aa)$ , $(Bb)$ et $(Cc)$ sont concourantes si et seulement si $\dfrac{\overline{aB}}{\overline{aC}}\times\dfrac{\overline{bC}}{\overline{bA}}\times\dfrac{\overline{cA}}{\overline{cB}}=-1$

Rendered by QuickLaTeX.com

La première démonstration utilise le « théorème du chevron »

$\bullet$ Soit $ABC$ un triangle, $Q$ un point de $(CB)$ et $P$ un point de $(AQ)$ , alors $\dfrac{\overline{QC}}{\overline{QB}}=\dfrac{\mathscr{A}(QCA)}{\mathscr{A}(QBA)}$ …. $=\dfrac{\mathscr{A}(QCP)}{\mathscr{A}(QBP)}$ pour les mêmes raisons… $=\dfrac{\mathscr{A}(PCA)}{\mathscr{A}(PBA)}$ par différence (chevron)
On utilise le fait que ces triangles ont le même hauteur.

Rendered by QuickLaTeX.com

Le théorème se démontre alors facilement :

En effet : $\dfrac{\overline{aB}}{\overline{aC}}=\dfrac{\mathscr{A}(OBA)}{\mathscr{A}(OCA)}$ , $\dfrac{\overline{bC}}{\overline{bA}}=\dfrac{\mathscr{A}(OCB)}{\mathscr{A}(OAB)}$ et $\dfrac{\overline{cA}}{\overline{cB}}=\dfrac{\mathscr{A}(OAC)}{\mathscr{A}(OBC)}$ ( chevron et rechevron et ..)

La loi des sinus permet aussi de démontrer le théorème de Céva :

Soit ABC un triangle et O le centre de son cercle circonscrit de rayon $R$ , D le point diamétralement opposé à B.

Rendered by QuickLaTeX.com

$(\overrightarrow{DC},\overrightarrow{DB})=(\overrightarrow{AC},\overrightarrow{AB})$ et donc $BC=2R \sin \hat{A}$

De même que $AC=2R \sin \hat{B}$ et $AB=2R \sin \hat{C}$ .

On en déduit $\dfrac{BC}{\sin\hat{A}}=\dfrac{AC}{\sin\hat{B}}=\dfrac{AB}{\sin\hat{C}}$

Le théorème se démontre alors ainsi:

Il suffit de considérer les trois triangles $OAB$ , $BOC$ et $COA$ qui ont pour sommet $O$ .

$\dfrac{OB}{OA}=\dfrac{\sin\hat{OAB}}{\sin\hat{OBA}}$ , $\dfrac{OC}{OB}=\dfrac{\sin\hat{OBC}}{\sin\hat{OCB}}$ , $\dfrac{OA}{OC}=\dfrac{\sin\hat{OCA}}{\sin\hat{OAC}}$
ce qui donne:

$\dfrac{\sin\hat{OAB}}{\sin\hat{OBA}}$ . $\dfrac{\sin\hat{OBC}}{\sin\hat{OCB}}$ . $\dfrac{\sin\hat{OCA}}{\sin\hat{OAC}}=1$

soit $\dfrac{\sin\hat{aAB}}{\sin\hat{bBA}}$ . $\dfrac{\sin\hat{bBC}}{\sin\hat{cCB}}$ . $\dfrac{\sin\hat{cCA}}{\sin\hat{aAC}}=-1$ en tenant compte maintenant de l’orientation des angles.

Puis comme $\dfrac{aB}{aC}=\dfrac{\sin\hat{aAB}}{\sin\hat{aAC}}.\dfrac{AB}{AC}$ et idem pour $\dfrac{bC}{bA}$ et $\dfrac{cA}{cB}$ le résultat s’ensuit.

Premières applications:

Soit ABC un triangle quelconque, les hauteurs issues de A, B et C sont concourantes .

Rendered by QuickLaTeX.com

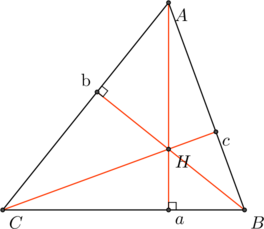
En effet $aB=AB\times \cos \widehat{B}$ , $aC=AC\times \cos \widehat{C}$ , $cB=CB\times \cos \widehat{B}$ …
Et finalement, on trouve bien $\dfrac{\overline{aB}}{\overline{aC}}\times\dfrac{\overline{bC}}{\overline{bA}}\times\dfrac{\overline{cA}}{\overline{cB}}=-1$

Pour les médianes, leur concours est évident car $\dfrac{\overline{aB}}{\overline{aC}}=-1=\dfrac{\overline{bC}}{\overline{bA}}=\dfrac{\overline{cA}}{\overline{cB}}$

Rendered by QuickLaTeX.com

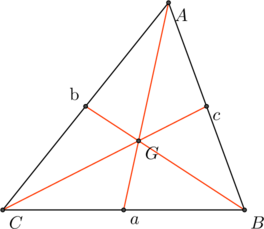
On remarquera cependant que le théorème du chevron énoncé plus haut permet de démontrer que les médianes partagent le triangle en six triangles de même aire, donc
$\mathscr{A}(AGB)=2\mathscr{A}(aBG)$ et ce même théorème permet de conclure que $AG=2Ga$ .

Pour les bissectrices d’un triangle,on utilisera cette propriété très pratique, conséquence de la loi des sinus, à savoir qu’une bissectrice intérieure de l’angle d’un triangle divise le côté opposé proportionnellement aux longueurs des côtés adjacents.

Rendered by QuickLaTeX.com

$\dfrac{Ca}{aB}=\dfrac{AC}{AB}$ et on obtient alors rapidement $\dfrac{\overline{aB}}{\overline{aC}}\times\dfrac{\overline{bC}}{\overline{bA}}\times\dfrac{\overline{cA}}{\overline{cB}}=-1$

Une autre façon de démontrer le théorème de Céva.

Notons $f$ , $g$ et $h$ les équations respectives des droites $(Aa)$ , $(Bb)$ et $(Cc)$

La relation essentielle : $[A,B, C] [f, g, h] = f(A)g(B)h(C) + f(B)g(C)h(A) + f(C)g(A)h(B)$
$-f(C)g(B)h(A) - f(B)g(A)h(C) - f(A)g(C)h(B)$ permet de démontrer directement le théorème, en effet :

Si les droites $(Aa)$ , $(Bb)$ et $(Cc)$ sont concourantes alors $[f, g, h]=0$ , comme de plus $f(A)=g(B)=h(C)=0$ alors
$f(B)g(C)h(A) + f(C)g(A)h(B)=0$
soit $\dfrac{f(B)g(C)h(A) }{f(C)g(A)h(B)}=-1$ (*)
Mais rappelons qu’en géométrie projective, si $D$ est une droite affine d’équation $f$ et soient a, b deux
points distincts du plan , on suppose que $D$ coupe (ab) en m, alors on a la
propriété suivante :

$\dfrac{\overline{ma}}{\overline{mb}}=\dfrac{f(a)T(b)}{f(b)T(a)}$ où $T$ est l’équation de { $D_{\infty}$ .

donc
$\dfrac{\overline{aB}}{\overline{aC}}\times\dfrac{\overline{bC}}{\overline{bA}}\times\dfrac{\overline{cA}}{\overline{cB}}=\dfrac{f(B)T(C)}{f(C)T(B)}\times\dfrac{g(C)T(A)}{g(A)T(C)}\times\dfrac{h(A)T(B)}{h(B)T(A)}=$
$\dfrac{f(B)}{f(C)}\times\dfrac{g(C)}{g(A)}\times\dfrac{h(A))}{h(B)}=-1$ d’après (*)

Le théorème de Céva se démontre aussi à l’aide du théorème de Ménélaüs, en effet:

Une journée sans Maths …