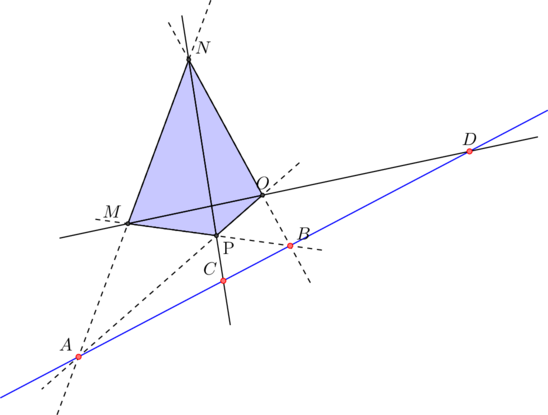
La division harmonique
Soient ![]() quatre points distincts d’une droite projective .
quatre points distincts d’une droite projective .
On dit que ces points forment une division harmonique si on a
![]() . (*)
. (*)
![]()
![]() et
et ![]() divisent alors le segment
divisent alors le segment ![]() dans le même rapport.
dans le même rapport.
La formule ![Rendered by QuickLaTeX.com [a,b,c,d]=\dfrac{\dfrac{1}{\overline{ab}}-\dfrac{1}{\overline{ad}}}{\dfrac{1}{\overline{ab}}-\dfrac{1}{\overline{ac}}}](https://www.math2.fr/wp-content/ql-cache/quicklatex.com-338f8520a639aa77f8f2a203d10910ef_l3.png) obtenue dans la partie 1 donne alors si
obtenue dans la partie 1 donne alors si ![]() :
:
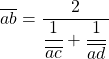
la longueur ![]() est la moyenne harmonique des longueurs
est la moyenne harmonique des longueurs ![]() et
et ![]() .
.
Soit ![]() un point quelconque et
un point quelconque et ![]() une division harmonique.
une division harmonique.
![]() ,
, ![]() etc.. et la relation * devient alors:
etc.. et la relation * devient alors:
![]()
Ce qui s’écrit avec ![]() milieu de [
milieu de [![]() ] et
] et ![]() milieu de [
milieu de [![]() ]:
]:
![]()
Posons ![]() cette relation devient
cette relation devient ![]() et comme
et comme ![]()
![]()
Posons ![]() et cette relation devient
et cette relation devient ![]()
Soit « le produit des distances à ![]() est égale au produit de la moyenne harmonique (
est égale au produit de la moyenne harmonique (![]() !) par la distance moyenne (
!) par la distance moyenne (![]() !) »
!) »
Voir l’ANNEXE à la fin de l’article pour les situations les plus classiques de rapport harmonique.
Retour sur la division homographique
Soient ![]() quatre points de
quatre points de ![]() et
et ![]() quatre points de
quatre points de ![]() , ces deux droites sont divisées homographiquement si et seulement si
, ces deux droites sont divisées homographiquement si et seulement si ![]() .
.
On a alors: ![]()
Soit ![]() un pont quelconque et
un pont quelconque et ![]() sont correspondant, on a alors
sont correspondant, on a alors ![]() .
.
Soit ![]() et
et ![]() son correspondant
son correspondant ![]() et de même si
et de même si ![]() , en nommant
, en nommant ![]() son correspondant, la division homographique s’exprime sous la forme :
son correspondant, la division homographique s’exprime sous la forme :
![]() et finalement la relation ci-dessous exprime la division homographique de deux droites:
et finalement la relation ci-dessous exprime la division homographique de deux droites:
![]()

Supposons maintenant que les droites sont positionnées de telle sorte que ![]()
Les points doubles (![]() ) sont les solutions d’une équation du type:
) sont les solutions d’une équation du type:
![]()

…et le milieu des points doubles coïncide avec le milieu de ![]() et en désignant par O ce point milieu cette équation devient:
et en désignant par O ce point milieu cette équation devient:
![]()
Si on choisit comme origine le point ![]() cette équation devient
cette équation devient ![]()
de sorte que les points doubles se situent de part et d’autre du point O à des distances égales à ![]()
Quand ![]() et
et ![]() ne se trouvent pas du même côté de
ne se trouvent pas du même côté de ![]() , les points doubles sont imaginaires.
, les points doubles sont imaginaires.
Si l’un des points doubles est à l’![]() on a alors
on a alors ![]() et la construction suivante permet d’obtenir très simplement le point double:
et la construction suivante permet d’obtenir très simplement le point double:
On considère l’intersection ![]() des deux cercles circonscrits aux triangles
des deux cercles circonscrits aux triangles ![]() et
et ![]() ,
, ![]() étant quelconque, ces deux cercles se recoupent en
étant quelconque, ces deux cercles se recoupent en ![]() et la corde
et la corde ![]() passera par le point double .
passera par le point double .

La division homographique de deux droites pourra s’écrire de différentes manières:
![]() (
(![]()
![]()
![]()
Involution:
Trois couples ![]() ,
,![]() et
et ![]() de points sont dits en involution si le birapport de quatre quelconque d’entre eux est égale au birapport de leur conjugué.
de points sont dits en involution si le birapport de quatre quelconque d’entre eux est égale au birapport de leur conjugué.
Exemple ![]()
On a alors ![]()
ou écrit différemment: ![]()
Si ![]() est à l’infini et soit
est à l’infini et soit ![]() sont conjugué, on a alors:
sont conjugué, on a alors:
![]() ou
ou ![]()
On appelle point double tout point coïncidant avec son conjugué,
On a alors ![]()
on appelera ![]() et
et ![]() les deux solutions mais alors:
les deux solutions mais alors:
![]() ce qui signifie que
ce qui signifie que ![]() et
et ![]() divisent harmoniquement
divisent harmoniquement ![]() et
et ![]() .
.
Si les trois couples ![]() ,
,![]() et
et ![]() sont en involution ainsi que
sont en involution ainsi que ![]() ,
,![]() et
et ![]() alors
alors ![]() ,
,![]() et
et ![]() le sont aussi donc si
le sont aussi donc si ![]() ,
,![]() et
et ![]() sont en involution,
sont en involution, ![]() . Et nous appellerons point central ce point remarquable .
. Et nous appellerons point central ce point remarquable .
Deux segments ![]() et
et ![]() étant placés sur une droite
étant placés sur une droite ![]() , la droite joignant les points d’intersection des deux cercles de diamètres
, la droite joignant les points d’intersection des deux cercles de diamètres ![]() et
et ![]() coupe
coupe ![]() en
en ![]() .
.
Si les deux segments n’empiètent pas l’un sur l’autre, on utilisera un point g quelconque et la droite joignant les deux points d’intersection des cercles circonscrits aux triangles ![]() et
et ![]() coupe la droite
coupe la droite ![]() en
en ![]() .
.
…autrement dit, les trois cercles ayant pour diamètres trois segments en involution passent par deux même point.
…ou encore, les segments définis par la rotation d’un angle droit autour d’un point fixe sur une droite quelconque sont en involution.
Notons pour finir que si ![]() ,
,![]() et
et ![]() sont en involution les deux points doubles définis ci-dessus divisent harmoniquement les trois segments
sont en involution les deux points doubles définis ci-dessus divisent harmoniquement les trois segments ![]() ,
, ![]() et
et ![]() et que ces deux points se situent à égale distance du point central.
et que ces deux points se situent à égale distance du point central.
Construction des points doubles:


Soient deux couples ![]() et
et ![]() de points conjugués, et
de points conjugués, et ![]() un cinquième point, soit
un cinquième point, soit ![]() un point extérieur et
un point extérieur et ![]() le deuxième point d’intersection des cercles circonscrits aux triangles
le deuxième point d’intersection des cercles circonscrits aux triangles ![]() et
et ![]() , le cercle circonscrits au triangle
, le cercle circonscrits au triangle ![]() recoupera la boite
recoupera la boite ![]() en
en ![]() , sixième point de l’involution.
, sixième point de l’involution.
Si les trois couples ![]() ,
,![]() et
et ![]() sont en involution, soit un
sont en involution, soit un ![]() un point quelconque sur la même droite, on aura avec les milieux
un point quelconque sur la même droite, on aura avec les milieux ![]() ,
, ![]() et
et ![]() des segmenst
des segmenst ![]() ,
, ![]() et
et ![]() l’équation:
l’équation:
![]()
Avec ![]() à l’infini, le point
à l’infini, le point ![]() sera le point central et l’équation ci-dessus devient:
sera le point central et l’équation ci-dessus devient:
![]()
ANNEXE
Voici quelques configurations classiques de rapports harmoniques:
![]() Dans un trapèze, la droite parallèle à la base passant par le point d’intersection des diagonales coupe les côtés en
Dans un trapèze, la droite parallèle à la base passant par le point d’intersection des diagonales coupe les côtés en ![]() et
et ![]() et la longueur
et la longueur ![]() est la moyenne harmonique des longueurs des bases.
est la moyenne harmonique des longueurs des bases.

![]() Soit
Soit ![]() une droite issue de
une droite issue de ![]() coupant
coupant ![]() en
en ![]() ,
, ![]() en
en ![]() et la polaire de A par rapport aux droites
et la polaire de A par rapport aux droites ![]() et
et ![]() en
en ![]() , alors
, alors ![]()
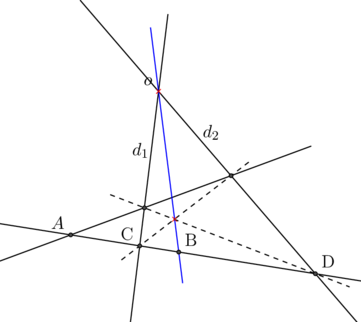
![]() Les bissectrices de l’angle
Les bissectrices de l’angle ![]() coupent
coupent ![]() en
en ![]() et
et ![]() et alors
et alors ![]()
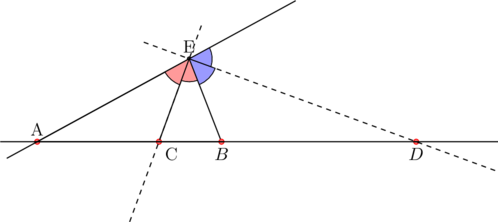
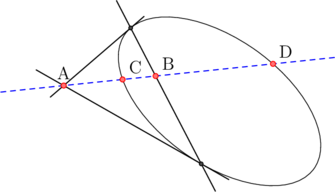
![]() Soit
Soit ![]() une droite issue de
une droite issue de ![]() coupant l’éllipse en
coupant l’éllipse en ![]() et
et ![]() et la polaire de A en
et la polaire de A en ![]() , alors
, alors ![]()
![]()
![]() un quadrilarère,
un quadrilarère, ![]() et
et ![]() les points d’intersection des diagonales avec la droite
les points d’intersection des diagonales avec la droite ![]() définie par les points d’intersection des côtés opposés, alors
définie par les points d’intersection des côtés opposés, alors ![]()