Deux autres présentations pour la multiplication et le problème des trois vases:
Multiplication,
![]() … On dispose les nombres comme indiqué ci-dessous, à l’intersection de chaque ligne et de chaque colonne, on indique le produit correspondant puis on ajoute les nombres présents dans chaque diagonale en partant du haut à droite sans oublier de reporter les éventuelles retenues dans la diagonale suivante. Pour finalement lire le résultat qui se lit de bas en haut….et obtenir
… On dispose les nombres comme indiqué ci-dessous, à l’intersection de chaque ligne et de chaque colonne, on indique le produit correspondant puis on ajoute les nombres présents dans chaque diagonale en partant du haut à droite sans oublier de reporter les éventuelles retenues dans la diagonale suivante. Pour finalement lire le résultat qui se lit de bas en haut….et obtenir ![]()

Un autre exemple : ![]()

….20833 !
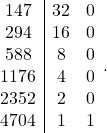
Soient à multiplier 147 et 32:
les nombres sont placés l’un en face de l’autre,on multiplie par 2 dans la colonne de gauche et on divise par deux dans la colonne de droite, si un nombre ![]() de la colonne de droite est impair, on place un
de la colonne de droite est impair, on place un ![]() dans une troisième colonne et on poursuit le calcul avec
dans une troisième colonne et on poursuit le calcul avec ![]() , sinon on place dans la troisième colonne le nombre 0 et on réitère le procédé.
, sinon on place dans la troisième colonne le nombre 0 et on réitère le procédé.
Le résultat est alors la somme des nombres de la première colonne ou apparaissent le 1 en fin de ligne.
![]() :
:

![]()
on remarquera que la troisième colonne fait apparaitre de bas en haut l’écriture de deuxième nombre en base ![]() , ce qui dispense de compléter la deuxième colonne..
, ce qui dispense de compléter la deuxième colonne..
![]() :
:
![]() s’écrit en base
s’écrit en base ![]() : 11001 donc :
: 11001 donc :

![]() .
.
Le problème des trois vases
Rappelons pour commencer que dans un triangle équilatéral, la somme des distances ![]() ,
, ![]() et
et ![]() d’un point
d’un point ![]() quelconque aux cotés du triangle est constamment égale à
quelconque aux cotés du triangle est constamment égale à ![]() , la hauteur du triangle.
, la hauteur du triangle.

En effet
![]()
![]()
![]()
![]() ,
, ![]() et
et ![]() forment alors un système de coordonnées du point
forment alors un système de coordonnées du point ![]() , les cotés
, les cotés ![]() ,
, ![]() et
et ![]() ont pour équations respectives
ont pour équations respectives ![]() ,
, ![]() et
et ![]() et les trois sommets ont pour coordonnées
et les trois sommets ont pour coordonnées ![]() ,
, ![]() et
et ![]() .
.
Les conditions suivantes :
![]() ,
, ![]() et
et ![]() assujettissent alors le point
assujettissent alors le point ![]() à se trouver dans le domaine hachuré ci-dessous:
à se trouver dans le domaine hachuré ci-dessous:
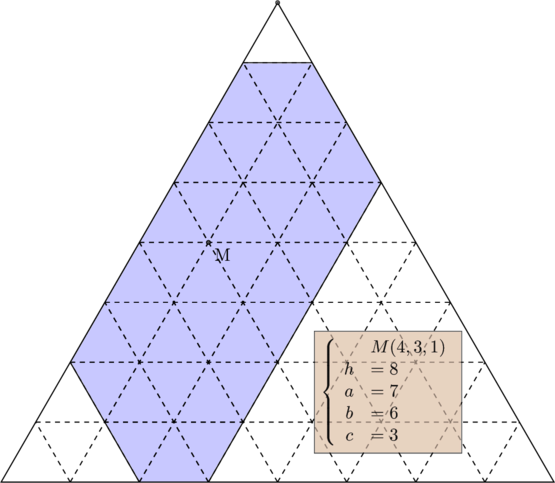
Et lorsque l’une des coordonnées du point ![]() est fixe, faire varier les deux autres revient à déplacer le point
est fixe, faire varier les deux autres revient à déplacer le point ![]() sur une droite parallèle à l’un des côtés du triangle.
sur une droite parallèle à l’un des côtés du triangle.
Soit maintenant le problème suivant:
Etant donnés ![]() litres d’un liquide répartis dans trois vases de contenances respectives
litres d’un liquide répartis dans trois vases de contenances respectives ![]() ,
, ![]() et
et ![]() litres, est -il possible de passer d’une répartition initiale
litres, est -il possible de passer d’une répartition initiale ![]() à la répartition
à la répartition ![]() ?
?
Une solution du problème correspond, avec le modèle présenté ci-dessus, à un chemin joignant les points de coordonnées ![]() et
et ![]() passant par les parallèle aux côtés du triangle. Passer par exemple du point
passant par les parallèle aux côtés du triangle. Passer par exemple du point ![]() au point
au point ![]() correspond au fait de remplir le vase 2 à l’aide du vase 1, dans lequel il ne restera plus que 1 litre !
correspond au fait de remplir le vase 2 à l’aide du vase 1, dans lequel il ne restera plus que 1 litre !
Exemple:On dispose d’un grand récipient plein, « la réserve », disons dix litres et de deux récipients de 3 et 5 litres. Le but est d’obtenir exactement 4 litres dans le récipient de 5 litres. Nous allons chercher à joindre, comme indiqué sur le schéma ci-dessous, les points de coordonnées (10,0,0) et (6,0,4) en restant dans la domaine ![]() ,
, ![]() et
et ![]() .
.
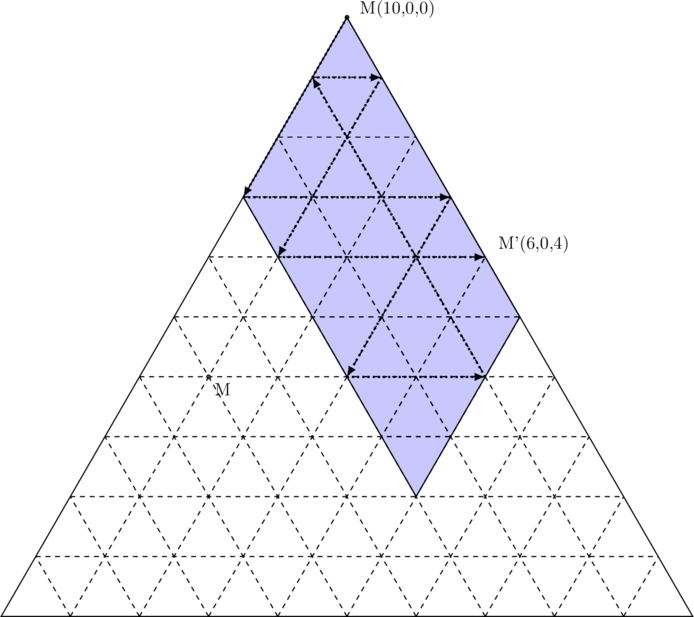
Soit un total de 8 transvasements……