Résumé:
![]() On se donne
On se donne
une forme linéaire non nulle ![]() et on considère l’hyperplan vectoriel
et on considère l’hyperplan vectoriel ![]() défini par T. On pose
défini par T. On pose ![]() (c’est un hyperplan projectif) et
(c’est un hyperplan projectif) et ![]()
L’application qui à ![]() et
et ![]() associe
associe ![]() est bien définie. C’est une opération de
est bien définie. C’est une opération de ![]() sur X , simplement transitive, de sorte qu’elle fait de
sur X , simplement transitive, de sorte qu’elle fait de ![]() un espace affine sous
un espace affine sous ![]() .
.
Si ![]() ,
, ![]() sont deux points de X, le vecteur
sont deux points de X, le vecteur ![]() est le vecteur de
est le vecteur de ![]() défini par
défini par ![]() , il est indépendant du choix des représentants des points.
, il est indépendant du choix des représentants des points.
Situation 1 (T=x+y+z)
Soit ![]() et
et ![]() ,
, ![]()
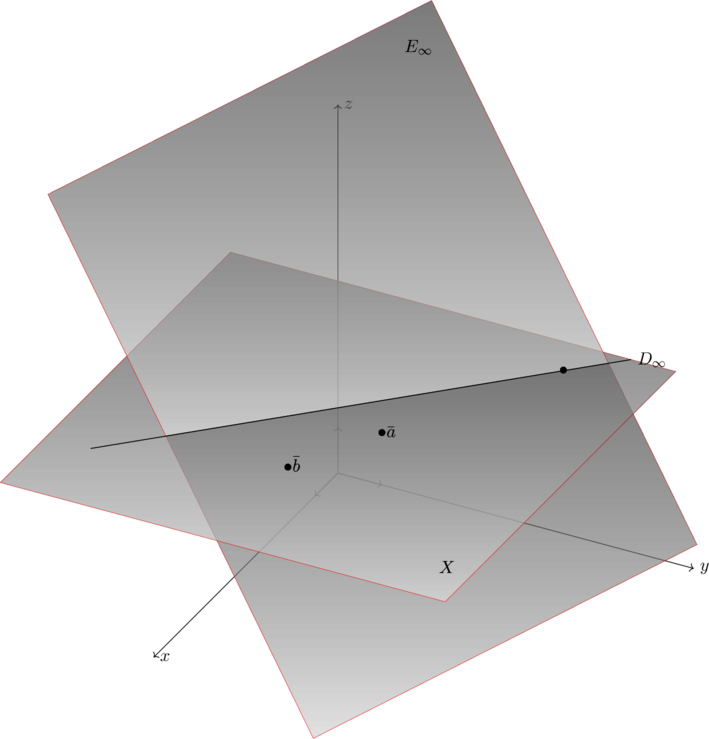
Soient ![]() deux points de
deux points de ![]() , la formule
, la formule ![]() définit une forme linéaire sur
définit une forme linéaire sur ![]() qui est une équation de
qui est une équation de ![]()
Pour ![]() dans
dans ![]() , le vecteur
, le vecteur ![]() de
de ![]() défini par la formule
défini par la formule ![]() aura pour image dans
aura pour image dans ![]() le point d’intersection des deux droites définies par
le point d’intersection des deux droites définies par ![]() et
et ![]() .
.
Une formule fondamentale :![]() .
.
![]() On appelle droite affine la trace sur
On appelle droite affine la trace sur![]() d’une droite projective distincte de
d’une droite projective distincte de ![]() . Une telle droite
. Une telle droite ![]() est l’image d’un plan vectoriel
est l’image d’un plan vectoriel ![]() de E, distinct de
de E, distinct de ![]() . La droite vectorielle associée est l’intersection
. La droite vectorielle associée est l’intersection
![]() et son image dans
et son image dans ![]() est l’unique point à l’infini de
est l’unique point à l’infini de ![]() (appelé
(appelé ![]() de D).
de D).
Situation 1 (T=x+y+z)
Soit ![]() et
et ![]()
![]() donne l’équation de
donne l’équation de ![]() soit
soit ![]() , et pour déterminer la direction ,comme :
, et pour déterminer la direction ,comme :
![]() , la direction de
, la direction de ![]() sera le point de
sera le point de ![]()
![]() ,
,
Deux droites ![]() et
et ![]() sont dites parallèles si les droites projectives associées ont même point à l’infini.
sont dites parallèles si les droites projectives associées ont même point à l’infini.
Soit ![]() l’équation de
l’équation de ![]() et
et ![]() ,
, ![]() les droites d’équations
les droites d’équations ![]() et
et ![]() . Les droites
. Les droites ![]() ,
, ![]() sont parallèles si et seulement si on a
sont parallèles si et seulement si on a ![]() .
.
Si f est une forme définissant une droite ![]() et si a, b sont deux points, les droites
et si a, b sont deux points, les droites ![]() et (ab) sont parallèles si et seulement si on a
et (ab) sont parallèles si et seulement si on a ![]() .
.
![]() Dans le plan affine, on peut définir (indépendamment de toute structure métrique) la
Dans le plan affine, on peut définir (indépendamment de toute structure métrique) la ![]() d’un vecteur de direction donnée.
d’un vecteur de direction donnée.
On suppose qu’on s’est donné une équation ![]() de
de ![]() . Alors, le vecteur
. Alors, le vecteur ![]() est un vecteur non nul de
est un vecteur non nul de![]() (qu’on appelle un
(qu’on appelle un ![]() de D), et si a, b sont deux points de
de D), et si a, b sont deux points de ![]() , on appelle mesure algébrique du vecteur
, on appelle mesure algébrique du vecteur ![]() relativement à
relativement à ![]() le nombre
le nombre ![]() défini par la formule :
défini par la formule : ![]()
Exemples : situation 1 (![]() )
)
Calcul du birapport: (voir article du même nom)
Soient ![]() ,
,![]() ,
,![]() ,
,![]() , quatre points de la droite
, quatre points de la droite ![]() image d’un plan vectoriel
image d’un plan vectoriel ![]() d’équation
d’équation ![]() ,
, ![]() .
.
Méthode 1 : (la plus courante)
![]()
Méthode 2 : Si ![]() est muni d’une base
est muni d’une base ![]() ,
, ![]() , et si les vecteurs image de ces points ont pour coordonnées respectives
, et si les vecteurs image de ces points ont pour coordonnées respectives ![]() ,
,![]() ,
,![]() et
et ![]() dans cette base, on a aussi :
dans cette base, on a aussi :
![Rendered by QuickLaTeX.com [a,b,c,d]=\dfrac{\begin{bmatrix}c_1 & a_1 \\c_2 & a_2\end{bmatrix}.\begin{bmatrix}d_1 & b_1 \\d_2 & b_2\end{bmatrix} }{\begin{bmatrix}c_1 & b_1 \\c_2 & b_2\end{bmatrix}.\begin{bmatrix}d_1 & a_1 \\d_2 & a_2\end{bmatrix}}](https://www.math2.fr/wp-content/ql-cache/quicklatex.com-6a9369b02004873200ecf5e35c24d7db_l3.png)
Méthode 3 : (Très pratique )
Si ![]() et
et ![]() sont les équations de deux droites passant par
sont les équations de deux droites passant par ![]() et
et ![]() , alors:
, alors:
![]()
Vérification :
![]() et
et ![]() est un vecteur directeur de
est un vecteur directeur de ![]() .
.
![]()
![]()
donc ![]()
![]()
![]()
donc ![]()
On aura aussi , ![]() et
et ![]() et pour finir:
et pour finir:
![Rendered by QuickLaTeX.com [a,b,c,d]=\dfrac{-\dfrac{3}{56}}{-\dfrac{7}{98}}\div\dfrac{-\dfrac{1}{104}}{-\dfrac{5}{182}}=\dfrac{15}{7}](https://www.math2.fr/wp-content/ql-cache/quicklatex.com-fb4a317c01c238ff7d133317d3b4c007_l3.png)
Pour la méthode 2 on choisit ![]() ,
, ![]() comme base de
comme base de ![]()
Considérons maintenant les vecteurs, ![]() image de
image de ![]() ,
, ![]() a pour coordonnées dans (
a pour coordonnées dans (![]() ,
, ![]() ),
), ![]() ,
, ![]() aura pour coordonnées
aura pour coordonnées ![]() ,
, ![]()
![]() et
et ![]()
![]()
donc ![Rendered by QuickLaTeX.com [a,b,c,d]=\dfrac{\begin{bmatrix}3 & 1.5 \\1& 1\end{bmatrix}.\begin{bmatrix}5 & 2.5 \\1 & 1\end{bmatrix} }{\begin{bmatrix}3 & 2.5 \\1& 1\end{bmatrix}.\begin{bmatrix}5 & 1.5 \\1 & 1\end{bmatrix}}=\dfrac{1.5 \times 2.5}{3.5 \times 0.5}=\dfrac{15}{7}](https://www.math2.fr/wp-content/ql-cache/quicklatex.com-4e95f072340f2f8e58fadcb931129b2d_l3.png) !
!
Pour illustrer la méthode 3, on choisit (au hasard ?) ![]() et
et ![]()
on a bien ![]() et
et
![]()
![]() .
.
Un autre exemple: parmi les applications projectives par excellence on trouve les incidences et les perspectives:
Soit ![]() une droite de
une droite de ![]() ) et
) et ![]() un point de
un point de ![]() , avec
, avec ![]() .
.
On appelle incidence l’ application ![]() qui à une droite
qui à une droite ![]() passant par
passant par ![]() , associe l’unique point d’ intersection de
, associe l’unique point d’ intersection de ![]() et de
et de ![]() , montrons à travers un exemple que cette application est une homographie.
, montrons à travers un exemple que cette application est une homographie.
Soit ![]() et
et ![]() ,
, ![]() a pour équation
a pour équation ![]() avec
avec ![]() soit
soit ![]()
Prenons ![]() et
et ![]() comme base de
comme base de ![]() , et
, et ![]() et
et ![]() comme base de
comme base de ![]() dont
dont ![]() est l’image, le point d’ intersection de
est l’image, le point d’ intersection de ![]() et de
et de ![]() est donné par le calcul
est donné par le calcul ![]()
![]()
![]() =
=![]()
…puis les coordonnées exactes du point d’intersection seront ![]()
Exemple, avec ![]() ,
, ![]() , les coordonnées du point cherché sont :
, les coordonnées du point cherché sont :
![]() !
!
![]() est bien une homographie car
est bien une homographie car ![]() où
où ![]() est l’application linéaire de
est l’application linéaire de ![]() dans
dans ![]() définie par
définie par
![]() =
=![]() .
.
On appelle perspective de centre ![]() de
de ![]() sur
sur ![]() .l’application
.l’application ![]() :
: ![]() qui à
qui à ![]() associe l’unique point d’ intersection de
associe l’unique point d’ intersection de ![]() et de
et de ![]() , montrons à travers un exemple que cette application est une homographie.
, montrons à travers un exemple que cette application est une homographie.
![]() ,
, ![]() et
et ![]() .
.
Prenons ![]() et
et ![]() comme base de
comme base de ![]() dont
dont ![]() est l’image , et
est l’image , et ![]() et
et ![]() comme base de
comme base de ![]() dont
dont ![]() est l’image
est l’image
Soit ![]() un point de
un point de ![]() et
et ![]() son image dans
son image dans ![]() ,
, ![]() aura pour équation
aura pour équation ![]()
![]()
![]()
Puis on calcule ![]() et on obtient
et on obtient ![]() =
=![]()
…puis les coordonnées exactes du point d’intersection seront ![]()
![]() est bien une homographie car
est bien une homographie car ![]() où
où ![]() est l’application linéaire de
est l’application linéaire de ![]() dans
dans ![]() définie par
définie par
la matrice ![]()
Remarque , on aurait pu remarquer qu’une perspective n’est rien d’autre que la composée de deux incidences…