Ci-dessous quelques démonstrations d’inspirations très diverses des formules clés de la trigonométrie .
CALCUL DE 
:
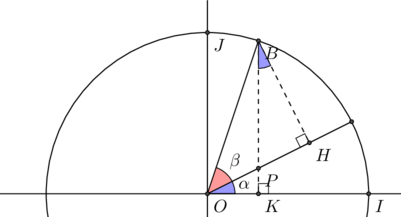
=OK=OP
PH=
OP+PH=
Continuer la lecture de Formules de duplication, cos(a+b), sin(a+b)….
LES ORIGINES DE LA LOI NORMALE
Ci dessous le long et douloureux calcul qui montre le lien entre loi binomiale et loi normale:
Point de départ, la formule de Stirling: 
.
Dans une suite de 
expériences, la probabilité d’obtenir 
et 
fois les évènement A et B est donné par: 
Le terme le plus grand du développement de 
correspond aux valeurs de et les plus voisinnes de 
et 
, donc on pose: 
et 
.
On a alors
et donc: 
Comme 
on obtient: 
Continuer la lecture de LES ORIGINES DE LA LOI NORMALE
Constructions au compas
Ci dessous , quelques exemples de constructions élémentaires,
au COMPAS SEUL.
Construction des angles 
, 
, 
, 
et 
:
Comment couper un arc de cercle en deux (sans bissectrice !!!):
Comment couper un segment en deux :
Théorème de Napoléon :
QCM de géométrie
[WATU 4]
Les configurations de référence de la géométrie dans l’espace.
Deux plans sécants et leur droite d’intersection:
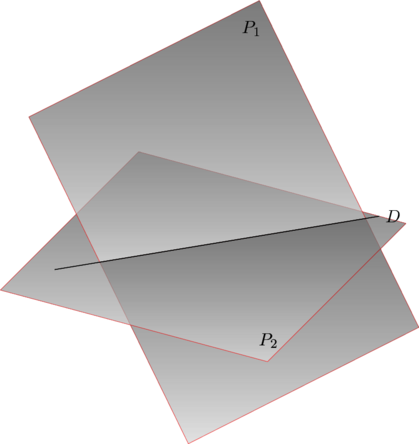
Deux plans parallèles coupés par un même troisième et les deux droites d’intersection parallèles.
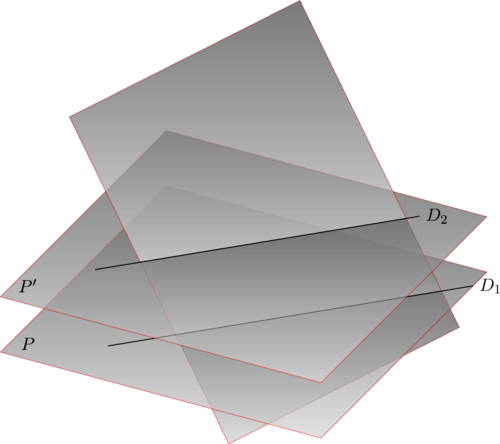
Une droite perpendiculaire à un plan et orthogonale à toute droite contenue dans ce plan.
Continuer la lecture de Les configurations de référence de la géométrie dans l’espace.