Ci dessous , vous trouverez différentes façons de démontrer le théorème de Céva ainsi que quelques applications évidentes
Le théorème de Céva :
a ,b et c étant trois points de ![]() ,
, ![]() et
et ![]() , les droites
, les droites ![]() ,
, ![]() et
et ![]() sont concourantes si et seulement si
sont concourantes si et seulement si ![]()

Ci dessous , vous trouverez différentes façons de démontrer le théorème de Céva ainsi que quelques applications évidentes
Le théorème de Céva :
a ,b et c étant trois points de ![]() ,
, ![]() et
et ![]() , les droites
, les droites ![]() ,
, ![]() et
et ![]() sont concourantes si et seulement si
sont concourantes si et seulement si ![]()

Pour commencer deux petits lemmes sur les aires :
![]() Soient
Soient ![]() et
et ![]() deux triangles tels que
deux triangles tels que ![]() et
et ![]() soient parallèles, alors
soient parallèles, alors ![]()
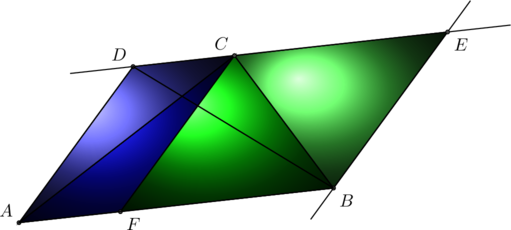
On trace les parrallèles à ![]() et
et ![]() , elles se coupent en
, elles se coupent en ![]() , et l’aire de chaque triangle est égale à la moitié de celle du parallèlogramme
, et l’aire de chaque triangle est égale à la moitié de celle du parallèlogramme ![]() .
.
![]() Soit
Soit ![]() un triangle,
un triangle, ![]() un point de
un point de ![]() et
et ![]() un point de
un point de ![]() , alors
, alors ![]() ….
…. ![]() pour les mêmes raisons…
pour les mêmes raisons… ![]() par différence (chevron)
par différence (chevron)
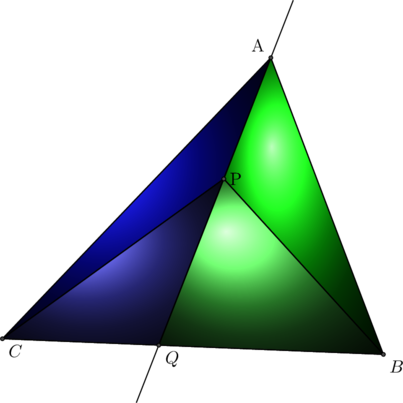
On utilise le fait que ces triangles ont le même hauteur.
Birapport de quatre points:
Définition:
Soit ![]() une droite projective et soient
une droite projective et soient ![]() quatre points de
quatre points de ![]() , avec
, avec ![]() distincts.
distincts.
Soit ![]() l’unique homographie de
l’unique homographie de ![]() sur
sur![]() définie par
définie par ![]() .
.
On appelle birapport des quatre points ![]() pris dans cet ordre l’élément
pris dans cet ordre l’élément ![]() et on le note [a,b,c,d].
et on le note [a,b,c,d].
Soit ![]() une homographie. On a l’égalité :
une homographie. On a l’égalité :
![]() .
.
Les perspectives seront par la suite des homographies particulièrement utilisées ainsi que les incidences : Soit ![]() une droite et
une droite et ![]() un point n’appartenant pas à
un point n’appartenant pas à ![]() . On appelle incidence l’ application qui à toute droite
. On appelle incidence l’ application qui à toute droite ![]() passant par
passant par ![]() associe l’unique point d’intersection
associe l’unique point d’intersection ![]() de
de ![]() et
et ![]() .
.
Calcul du birapport:
Soit ![]() une droite projective et soient
une droite projective et soient ![]() quatre points de
quatre points de ![]() , avec
, avec ![]() distincts, on a la formule suivante:
distincts, on a la formule suivante:
Continuer la lecture de Birapport (partie 1)
Ci-dessous quelques démonstrations d’inspirations très diverses des formules clés de la trigonométrie .
CALCUL DE ![]() :
:
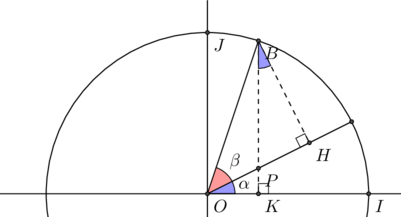
![]() =OK=OP
=OK=OP![]()
PH=![]()
OP+PH=![]()
Continuer la lecture de Formules de duplication, cos(a+b), sin(a+b)….
Ci dessous , quelques exemples de constructions élémentaires,
au COMPAS SEUL.
Construction des angles ![]() ,
, ![]() ,
, ![]() ,
, ![]() et
et ![]() :
:
Comment couper un arc de cercle en deux (sans bissectrice !!!):
Comment couper un segment en deux :
Théorème de Napoléon :